Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A ) => \(\Delta BMD=\Delta CNE\left(ch-gn\right)\) => BM = CN c) Ta có : \(\widehat{MBD}=\widehat{NCE}\) ( \(\Delta BMD=\Delta CNE\) ) mà \(\widehat{MBD}=\widehat{IBC},\widehat{NCE}=\widehat{ICB}\) ( 2 góc đối đỉnh ) => \(\widehat{IBC}=\widehat{ICB}\) => Tam giác IBC cân tại I d) \(\Delta IAB=\Delta IAC\left(c.c.c\right)\) => \(\widehat{IAB}=\widehat{IAC}\) => AI là tia phân giác của góc BAC
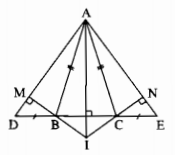
a) Xét ∆ADE cân tại A nên góc D = góc E
Xét ∆ABD và ∆ACE, ta có:
AD = AE (gt)
góc D = góc E (chứng minh trên)
DB = EC (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
b) Xét hai tam giác vuông BMD và CNE, ta có:
góc BMD=góc CNE=90o
BD = CE (gt)
góc D = góc E (chứng minh trên)
Suy ra: ∆BMD = ∆CNE (cạnh huyền, góc nhọn)
Suy ra: BM = CN (hai cạnh tương ứng)
c) Ta có: ∆BMD = ∆CNE (chứng minh trên)
Suy ra: góc DBM=góc ECN (hai góc tương ứng)
góc DBM=góc IBC (đối đỉnh)
góc ECN = góc ICB (đối đỉnh)
Suy ra: góc IBC=góc ICB hay ∆IBC cân tại I.
d) Xét ∆ABI và ∆ACI, ta có:
AB = AC (chứng minh trên)
IB = IC (vì ∆IBC cân tại I)
AI cạnh chung
Suy ra: ∆ABI = ∆ACI (c.c.c) ⇒ góc BAI=góc CAI (hai góc tương ứng)
Vậy AI là tia phân giác của góc BAC
a: Xet ΔABD và ΔACE có
AD=AE
góc D=góc E
DB=EC
=>ΔABD=ΔACE
=>AB=AC
=>ΔABC cân tại A
b: Xét ΔAMB vuông tại M và ΔANC vuông tại N có
AB=AC
góc MAB=góc NAC
=>ΔAMB=ΔANC
=>BM=CN
c: góc IBC=góc MBD
góc ICB=góc NCE
mà góc MBD=góc NCE
nên góc ICB=góc IBC
=>ΔIBC cân tại I
tu ve hinh :
a, tamgiac ADE can tai A (gt)
=> AD = AE va goc ADE = goc AED (dn)
xet tamgiac ADB va tamgiac AEC co : DB = CE (gt)
=> tamgiac ADB = tamgiac AEC (c - g - c)
=> AB = AC (dn)
=> tamgiac ABC can tai A (dn)
b, xet tamgiac DMB va tamgiac ENC co :
goc DMB = goc ENC = 90o do MB | AD va CN | AE (gt)
goc ADE = goc AED (cau a)
DB = CE (gt)
=> tamgiac DMB = tamgiac ENC (ch - gn)
=> BM = CN (dn)
Ta có hình vẽ sau:
a) Xét \(\Delta ADB\)và \(\Delta AEC\):
AD=AE(\(\Delta ADE\)cân tại A)
DB=EC(gt)
\(\widehat{ADB}=\widehat{AEC}\)(\(\Delta ADE\)cân tại A)
\(\Rightarrow\Delta ADB=\Delta AEC\left(c-g-c\right)\)
=> AB=AC(2 cạnh tương ứng)
=> \(\Delta ABC\)cân tại A
b) Xét \(\Delta MDB\)và \(\Delta NEC:\)
DB=EC(gt)
\(\widehat{MDB}=\widehat{NEC}\)(cm câu a)
\(\widehat{DMB}=\widehat{ENC}=90^o\)
\(\Rightarrow\Delta MDB=\Delta NEC\left(ch-gn\right)\)
=> MB=NE( 2 cạnh tương ứng)
=> Đpcm
c)Ta có \(\Delta MDB=\Delta NEC\)(cm câu b)
=> \(\widehat{MBD}=\widehat{NCE}\)( 2 góc tương ứng)
Mà \(\hept{\begin{cases}\widehat{MBD}=\widehat{CBI}\\\widehat{NEC}=\widehat{BCI}\end{cases}}\)( đối đỉnh)
\(\Rightarrow\widehat{CBI}=\widehat{BCI}\)
=> \(\Delta IBC\)cân tại I
d) Ta có \(\Delta IBC\)cân tại I
=> IB=IC
Xét \(\Delta ABI\)và \(\Delta ACI:\)
AB=AC(\(\Delta ABC\)cân tại A)
IB=IC(cmt)
AI: cạnh chung
\(\Rightarrow\Delta ABI=\Delta ACI\left(c-c-c\right)\)
=> \(\widehat{IAB}=\widehat{IAC}\)( 2 góc tương ứng)
=> AI là tia phân giác của \(\widehat{BAC}\)
=> Đpcm
P/s: đáng nhẽ xong lâu rồi, thì đúng lúc chuẩn bị up thì máy nó sập...-.-' , ko biết nói gì luôn)
Bài làm
a) Xét tam giác ABD và tam giác ACE có:
AD = AE ( Do tam giác ADE cân )
\(\widehat{D}=\widehat{E}\)( Do tam giác ADE cân )
BD = EC ( gt )
=> Tam giác ABD = tam giác ACE ( c.g.c )
=> AB = AC
=> Tam giác ABC cân tại A.
b) Vì tam giác ABD = tam giác ACE ( cmt )
BD = EC
Xét tam giác DMB và tam giác ENC có:
\(\widehat{DMB}=\widehat{ENC}=90^0\)
Cạnh huyền BD = EC
Góc nhọn: \(\widehat{D}=\widehat{E}\)
=> Tam giác DMB và tam giác ENC ( cạnh huyền - góc nhọn )
=> BM = CN
c) Vì tam giác DMB và tam giác ENC ( cmt )
=> \(\widehat{MBD}=\widehat{NCE}\)
Ta có: \(\widehat{MBD}=\widehat{IBC}\)( hai góc đối )
\(\widehat{NCE}=\widehat{BCI}\)
=> \(\widehat{IBC}=\widehat{BCI}\)
=> Tam giác IBC cân tại I.
d) Vì tam giác IBC là tam giác cân
=> IB = IC
Ta có: IB + BM = IM
CN + CI = IN
Mà IB = IC
BM = CN
=> IM = IN
Xét tam giác AMI và tam giác ANI có:
\(\widehat{AMI}=\widehat{ANI}=90^0\)
Cạnh huyền: AI
cạnh góc vuông: IM = IN
=> Tam giác AMI và tam giác ANI ( cạnh huyền - cạnh góc vuông )
=> \(\widehat{MAI}=\widehat{NAI}\)
=> AI là tia phân giác của góc MAN
Hay AI là tia phân giác của góc BAC ( đpcm )
# Học tốt #
a: Xét ΔADB và ΔAEC có
AB=AC
\(\widehat{ADB}=\widehat{AEC}\)
DB=EC
Do đó: ΔADB=ΔAEC
Suy ra: AB=AC
hay ΔABC cân tại A
b: Xét ΔMBD vuông tại M và ΔNCE vuông tại N có
BD=CE
\(\widehat{MDB}=\widehat{NEC}\)
Do đó: ΔMBD=ΔNCE
Suy ra: BM=CN
c: \(\widehat{IBC}=\widehat{MBD}\)(đối đỉnh)
\(\widehat{ICB}=\widehat{NCE}\)
mà \(\widehat{MBD}=\widehat{NCE}\)(ΔMBD=ΔNCE)
nên \(\widehat{IBC}=\widehat{ICB}\)
hay ΔIBC cân tại I
bớt spam