
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(tanx=-tan\dfrac{\pi}{5}\)
\(\Leftrightarrow tanx=tan\left(-\dfrac{\pi}{5}\right)\)
\(\Leftrightarrow x=-\dfrac{\pi}{5}+k\pi\)
Mình quên mất, nó nằm trong khoảng (π/2; π) nha, mình xin lỗi


6.
Gọi \(M\left(x;y\right)\) là điểm bất kì thuộc \(\Delta\Rightarrow x+5y-1=0\) (1)
Gọi \(M'\left(x';y'\right)\in\Delta'\) là ảnh của \(\Delta\) qua phép tịnh tiến nói trên
\(\Rightarrow\left\{{}\begin{matrix}x'=x+4\\y'=y+2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-4\\y=y'-2\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow x'-4+5\left(y'-2\right)-1=0\)
\(\Leftrightarrow x'+5y'-15=0\)
Hay ảnh của \(\Delta\) qua phép tịnh tiến nói trên là đường thẳng có pt: \(x+5y-15=0\)
7.
Gọi \(M\left(x;y\right)\in\Delta\)
Gọi \(M'\left(x';y'\right)\in\Delta'\Rightarrow2x'+y'-5=0\) (1)
Đồng thời M' là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\)
\(\left\{{}\begin{matrix}x'=x-4\\y'=y+2\end{matrix}\right.\)
Thế vào (1):
\(\Rightarrow2\left(x-4\right)+1\left(y+2\right)-5=0\)
\(\Leftrightarrow2x+y-11=0\)
Hay phương trình \(\Delta\) có dạng: \(2x+y-11=0\)


1.
\(\left(sinx+1\right)\left(sinx-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow sinx=-1\)
\(\Leftrightarrow x=-\dfrac{\pi}{2}+k2\pi\)
2.
\(sin2x\left(2sinx-\sqrt{2}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\2sinx-\sqrt{2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=0\\sinx=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{k\pi}{2}\\x=\dfrac{\pi}{4}+k2\pi\\x=\dfrac{3\pi}{4}+k2\pi\end{matrix}\right.\)

3.
\(4sinx+cosx+2cos\left(x+\dfrac{\pi}{3}\right)=2\)
\(\Leftrightarrow4sinx+cosx+cosx-\sqrt{3}sinx=2\)
\(\Leftrightarrow\left(4-\sqrt{3}\right)sinx+2cosx=2\)
\(\Leftrightarrow\sqrt{23-4\sqrt{3}}\left(\dfrac{4-\sqrt{3}}{\sqrt{23-4\sqrt{3}}}sinx+\dfrac{2}{\sqrt{23-4\sqrt{3}}}cosx\right)=2\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}\right)=\dfrac{2}{\sqrt{23-4\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}=\pm arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{2}{\sqrt{23-4\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)
4.
\(sinx+2cos\left(x+\dfrac{\pi}{3}\right)+4sin\left(x+\dfrac{\pi}{6}\right)+cosx=4\)
\(\Leftrightarrow sinx+cosx-\sqrt{3}sinx+2\sqrt{3}sinx+2cosx+cosx=4\)
\(\Leftrightarrow\left(1+\sqrt{3}\right)sinx+4cosx=4\)
\(\Leftrightarrow\sqrt{20+2\sqrt{3}}\left(\dfrac{1+\sqrt{3}}{\sqrt{20+2\sqrt{3}}}sinx+\dfrac{4}{\sqrt{20+2\sqrt{3}}}cosx\right)=4\)
\(\Leftrightarrow cos\left(x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}\right)=\dfrac{4}{\sqrt{20+2\sqrt{3}}}\)
\(\Leftrightarrow x-arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}=\pm arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2arccos\dfrac{4}{\sqrt{20+2\sqrt{3}}}+k2\pi\\x=k2\pi\end{matrix}\right.\)

\(y=\dfrac{cos3x}{1-sinx}+tanx=\dfrac{cos3x}{1-sinx}+\dfrac{sinx}{cosx}\)
Hàm số xác định khi \(\left\{{}\begin{matrix}1-sinx\ne0\\cosx\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}sinx\ne1\\cosx\ne0\end{matrix}\right.\Leftrightarrow x\ne\dfrac{\pi}{2}+k\pi\)

Điều kiện: \(n\ge3\)
Giả thiết tương đương:
\(\dfrac{n!}{\left(n-3\right)!.3!}-\dfrac{\left(n-1\right)!}{2!\left(n-3\right)!}=\dfrac{\left(n-1\right)!}{\left(n-2\right)!}.\dfrac{\left(n+3\right)!}{\left(n+2\right)!}\)
\(\Leftrightarrow\dfrac{n\left(n-1\right)\left(n-2\right)}{6}-\dfrac{\left(n-1\right)\left(n-2\right)}{2}=\left(n-1\right)\left(n+3\right)\)
\(\Leftrightarrow\dfrac{n\left(n-2\right)}{6}-\dfrac{n-2}{2}=n+3\)
\(\Leftrightarrow n^2-11n-12=0\Rightarrow\left[{}\begin{matrix}n=12\\n=-1\left(loại\right)\end{matrix}\right.\)
Vậy khai triển đã cho là: \(x^3\left(x^3-\dfrac{12}{3x}\right)^{12}=x^3\left(x^3-\dfrac{4}{x}\right)^{12}\)
Số hạng tổng quát trong khai triển:
\(C_{12}^k.\left(x^3\right)^k.\left(-\dfrac{4}{x}\right)^{12-k}.x^3=C_{12}^k.\left(-4\right)^{12-k}.x^{4k-9}\)
Số hạng chứa \(x^{11}\) thỏa mãn:
\(4k-9=11\Leftrightarrow k=5\)
Hệ số: \(C_{12}^5.\left(-4\right)^7=-C_{12}^5.4^7=...\)





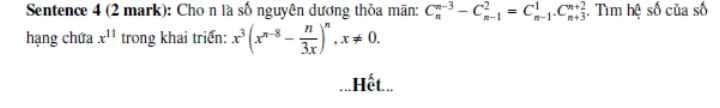
\(tan\left(\dfrac{x}{2}\right)=\sqrt{3}\)
\(\Leftrightarrow\dfrac{x}{2}=\dfrac{\pi}{3}+k\pi\)
\(\Leftrightarrow x=\dfrac{2\pi}{3}+k2\pi\) (\(k\in Z\))