K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
3 tháng 7 2017
\( x^4-2x^2-400x-9999=0 \)
\(\Leftrightarrow\)\( x^4+11x^3+ 119x^2+909x-11.(x^3+11x^2 +119x+909)=0 \)
\(\Leftrightarrow\) \((x-11).(x^3+11x^3 +119x+909)=0 \)
\(\Leftrightarrow\)\((x-11).(x^3+2x^2+ 101x+9x^2+ 18x+909)=0 \)
\(\Leftrightarrow\) \((x-11).(x+9).(x^2+ 2x+101)=0 \)
Vậy nghiệm của pt là \(11\) và \(-9\)
BH
20 tháng 2 2019
\(\frac{x+4}{\left(x-2\right)\left(2x-1\right)}+\frac{x+1}{\left(x-3\right)\left(2x-1\right)}=\frac{2x+5}{\left(x-3\right)\left(2x-1\right)}\)
\(\frac{\left(x-3\right)\left(x+4\right)}{\left(x-2\right)\left(2x-1\right)\left(x-3\right)}+\frac{\left(x+1\right)\left(x-2\right)}{\left(x-3\right)\left(2x-1\right)\left(x-2\right)}=\frac{\left(2x+5\right)\left(x-2\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1\right)}\)
\(\Rightarrow x^2+x-12+x^2-x-2=2x^2+x-10\Leftrightarrow x=-4\)
20 tháng 2 2019
\(\frac{x+4}{2x^2-5x+2}+\frac{x+1}{2x^2-7x+3}=\frac{2x+5}{2x^2-7x+3}\)
\(\Rightarrow\frac{x+4}{2x^2-5x+2}=\frac{2x-5}{2x^2-7x+3}-\frac{x+1}{2x^2-7x+3}\)
\(\Rightarrow\frac{x+4}{2x^2-5x+2}=\frac{x+4}{2x^2-7x+3}\)
TH1:\(x+4\ne0\)
\(\Rightarrow2x^2-5x+2=2x^2-7x+3\)
\(\Rightarrow-5x+2=-7x+3\)
\(\Rightarrow2x=1\)
\(\Rightarrow x=\frac{1}{2}\)
TH2:\(x+4=0\)
\(\Rightarrow x=-4\)
TN
1
26 tháng 1 2017
X^4-2x^2-400x-9999 <=>x^4+11x^3-11x^3+119x^2-121x^2+909x-1309x-9999=0 <=>x^4+11x^3+119x^2+909x-11(x^3+11x^2+119x+9999)<=>(x-11)(x^3+11x^2+119x+909) . Phân tích tiếp ta được (x-11)(x+9)(x^2+2x+101)
PT
1
CM
29 tháng 5 2019
(x + 2)( x 2 – 3x + 5) = (x + 2) x 2
⇔ (x + 2)( x 2 – 3x + 5) – (x + 2) x 2 = 0
⇔ (x + 2)[( x 2 – 3x + 5) – x 2 ] = 0
⇔ (x + 2)( x 2 – 3x + 5 – x 2 ) = 0
⇔ (x + 2)(5 – 3x) = 0
⇔ x + 2 = 0 hoặc 5 – 3x = 0
x + 2 = 0 ⇔ x = -2
5 – 3x = 0 ⇔ x = 5/3
Vậy phương trình có nghiệm x = -2 hoặc x = 5/3
PT
1
CM
7 tháng 12 2018
Điều kiện xác định: x ≠ ±2.
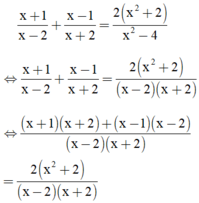
⇒ (x + 1)(x + 2) + (x – 1)(x – 2) = 2(x2 + 2)
⇔ x2 + x + 2x + 2 + x2 – x – 2x + 2 = 2x2 + 4
⇔ 2x2 + 4 = 2x2 + 4
⇔ 0x = 0.
Vậy phương trình nghiệm đúng với mọi x ≠ ±2.
HH
3
I
14 tháng 4 2021
Ta có:Giá trị tuyệt đối của một đa thức luôn luôn >=0
Mặt khác, ta có -2x2-2=-2(x2+1) luôn luôn <0(vì x2+1 >=1>0),(-2>0)
-->không thể có giá trị của x phù hợp
14 tháng 4 2021
Ta có: \(\left|2x^2-5x+3\right|=-2x^2-2\)
\(\Leftrightarrow\left|2x^2-5x+3\right|=-\left(2x^2+2\right)\)
mà \(\left|2x^2-5x+3\right|\ge0\forall x\)
và \(-\left(2x^2+2\right)< 0\forall x\)
nên \(x\in\varnothing\)
Vậy: \(S=\varnothing\)
CM
13 tháng 12 2019
Nếu đặt u = x 2 − 1 thì x 2 = u + 1 nên phương trình có dạng
( 2 + 2)u = 2(u + 1) − 2 (1)
Ta giải phương trình (1):
(1) ⇔ 2 u + 2u = 2u + 2 − 2
⇔ 2 u = 2 − 2
⇔ 2 u = 2 ( 2 − 1) ⇔ u = 2 − 1
⇔ x 2 − 1 = 2 − 1
⇔ x 2 = 2
⇔ x = 1
\(x^4-2x^2=400x+9999=0\)
\(\Leftrightarrow x^4+11x^3+119x^2+909x-11\left(x^3+11x^3+119x+909\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x^3+11x^2+119x+909\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x^3+2x^2+101x+9x^2+18x+909\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x+9\right)\left(x^2+2x+101\right)=0\)
\(\Rightarrow\orbr{\begin{cases}11\\-9\end{cases}}\)