
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-2x=2\sqrt{2x-1}\) \(\left(Đk:x\ge\dfrac{1}{2}\right)\)
\(x^2=2x+2\sqrt{2x-1}\)
\(x^2=2x-1+2\sqrt{2x-1}+1\)
\(x^2=\left(\sqrt{2x-1}+1\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2x-1}+1\\x=-\sqrt{2x-1}-1\end{matrix}\right.\)
+) \(x=\sqrt{2x-1}+1\)
\(x-1=\sqrt{2x-1}\left(x\ge1\right)\)
\(x^2-2x+1=2x-1\)
\(x^2-4x+2=0\)
\(\left(x-2\right)^2=2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{2}+2\left(TM\right)\\x=2-\sqrt{2}\left(L\right)\end{matrix}\right.\)
+) \(x=-\sqrt{2x-1}-1\)
VP\(\le-1\) mà \(VT\ge\dfrac{1}{2}\)
=> phương trình vô nghiệm
Vậy \(S=\left\{2+\sqrt{2}\right\}\)

Đặt \(\sqrt{x^2-2x+5}=t>0\)
\(\Rightarrow x^2-2x=t^2-5\)
Phương trình trở thành:
\(t=t^2-5-1\Leftrightarrow t^2-t-6=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-2\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-2x+5}=3\)
\(\Rightarrow x^2-2x+5=9\)
\(\Rightarrow x^2-2x-4=0\)
\(\Rightarrow...\)


A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-x1x2
=(1/2)^2-(-1/4)=1/4+1/4=1/2

TH1: \(\left\{{}\begin{matrix}2x-7\ge0\\2x-7< x^2+2x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{7}{2}\\x^2>-9\end{matrix}\right.\) \(\Rightarrow x\ge\dfrac{7}{2}\)
TH2: \(\left\{{}\begin{matrix}2x-7< 0\\7-2x< x^2+2x+2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}\\x^2+4x-5>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{7}{2}\\\left[{}\begin{matrix}x>1\\x< -5\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}1< x< \dfrac{7}{2}\\x< -5\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x>1\\x< -5\end{matrix}\right.\)

\(\Leftrightarrow\left(x^2-2x\right)^2+x^2-2x+1-13=0\)
\(\Leftrightarrow\left(x^2-2x\right)^2+x^2-2x-12=0\)
Đặt \(x^2-2x=t\Rightarrow t^2+t-12=0\Rightarrow\left[{}\begin{matrix}t=3\\t=-4\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x^2-2x=3\\x^2-2x=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-3=0\\x^2-2x+4=0\left(vô-nghiệm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)

(x2 + 2x – 5)2 = (x2 – x + 5)2
⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ [(x2 + 2x – 5) – (x2 – x + 5)].[(x2 + 2x – 5) + (x2 – x + 5)] = 0
⇔ (3x – 10)(2x2 + x ) = 0
⇔ (3x-10).x.(2x+1)=0
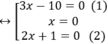
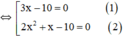
+ Giải (1): 3x – 10 = 0 ⇔ 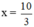
+ Giải (2):
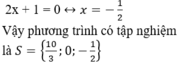


\(x^2-2x=2\sqrt{2x-1}\left(đk:x\ge0,5\right)\\ \Leftrightarrow x^4-4x^3+4x^2=4\left(2x-1\right)\\ \Leftrightarrow x^4-4x^3+4x^2=8x-4\\ \Leftrightarrow x^4-4x^3+4x^2-8x+4=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2+\sqrt{2}\left(tm\right)\\x=2-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{2-\sqrt{2};2+\sqrt{2}\right\}\)