Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,\left(2x-1\right)^2=49\)
\(\left[{}\begin{matrix}2x-1=7\\2x-1=-7\end{matrix}\right.\)
\(\left[{}\begin{matrix}2x=8\\2x=-6\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
\(b,\left(2x+7\right)^2=9\left(x+2\right)^2\)
\(4x^2+28x+49=9x^2+36x+36\)
\(4x^2+28x+49-9x^2-36x-36=0\)
\(-5x^2-8x+13=0\)
\(5x^2+13-5x-13=0\)
\(x\left(5x+13\right)-1\left(5x+13\right)=0\)
\(\left(x-1\right)\left(5x+13\right)=0\)
\(\left[{}\begin{matrix}x=1\\5x=-13\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=1\\x=-\frac{13}{5}\end{matrix}\right.\)
\(c,4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\left[2\left(2x+7\right)\right]^2-\left[3\left(x+3\right)\right]^2=0\)
\(\left(4x+14\right)^2-\left(3x+9\right)^2=0\)
\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(x=-5\)
\(d,\left(5x-3\right)^2-\left(4x-7\right)^2=0\)
\(25x^2-30x+9-16x^2+56x-49=0\)
\(9x^2+26x-40=0\)
\(9x^2+36x-10x-40=0\)
\(9x\left(x+4\right)-10\left(x+4\right)=0\)
\(\left(9x-10\right)\left(x+4\right)=0\)
\(\left[{}\begin{matrix}9x-10=0\\x+4=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\frac{10}{9}\\x=-4\end{matrix}\right.\)

a,(2x-1)^2=49
<=>(2x-1)^2=7^2
<=>(2x-1)^2-7^2=0
<=>(2x-1-7)(2x-1+7)=0
<=>(2x-8)(2x+6)=0
<=>2x-8=0 hoặc 2x+6=0
<=>x=4 hoặc x=-3
a) (2x - 1)2 - 49 = 0
⇔ (2x - 1 + 7)(2x - 1 - 7) = 0
⇔ (2x + 6)(2x - 8) = 0
⇔\(\left[{}\begin{matrix}2x+6=0\\2x-8=0\end{matrix}\right.\text{⇔}\left[{}\begin{matrix}x=-3\\x=4\end{matrix}\right.\)
Vậy nghiệm của pt là x = -3 và x = 4

a) \(\left(x+2\right)^2-9\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x+2\right)^2-\left(3x-6\right)^2=0\)
\(\Leftrightarrow\left(x+2+3x-6\right)\left(x+2-3x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(4x-4\right)=0\\\left(8-2x\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
b)\(4\left(2x+7\right)^2-9\left(x+3\right)^2=0\)
\(\Leftrightarrow\left(4x+14\right)^2-\left(3x+9\right)^2=0\)
\(\Leftrightarrow\left(4x+14-3x-9\right)\left(4x+14+3x+9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-\frac{23}{7}\end{matrix}\right.\)
c) \(\left(5x^2-2x+10\right)^2-\left(3x^2+10x-8\right)^2=0\)
\(\Leftrightarrow\left(5x^2-2x+10-3x^2-10x+8\right)\left(5x^2-2x+10+3x^2+10x-8\right)=0\)
\(\Leftrightarrow\left(2x^2-5x+18\right)\left(8x^2+8x+2\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\frac{1}{2}\\x=3\end{matrix}\right.\)

1) \(\left(5x-4\right)\left(4x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}5x-4=0\\4x-6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=4\\4x=6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{\dfrac{4}{5};\dfrac{3}{2}\right\}\)
2) \(\left(4x-10\right)\left(24+5x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}4x-10=0\\24+5x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}4x=10\\5x=-24\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=\dfrac{-24}{5}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{\dfrac{5}{2};\dfrac{-24}{5}\right\}\)
3) \(\left(x-3\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\2x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{3;\dfrac{-1}{2}\right\}\)

Bài 1:
a) (5x-4)(4x+6)=0
\(\Leftrightarrow\orbr{\begin{cases}5x-4=0\\4x+6=0\end{cases}\Leftrightarrow\orbr{\begin{cases}5x=4\\4x=-6\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{4}{5}\\y=\frac{-3}{2}\end{cases}}}\)
b) (x-5)(3-2x)(3x+4)=0
<=> x-5=0 hoặc 3-2x=0 hoặc 3x+4=0
<=> x=5 hoặc x=\(\frac{3}{2}\)hoặc x=\(\frac{-4}{3}\)
c) (2x+1)(x2+2)=0
=> 2x+1=0 (vì x2+2>0)
=> x=\(\frac{-1}{2}\)
bài 1:
a) (5x - 4)(4x + 6) = 0
<=> 5x - 4 = 0 hoặc 4x + 6 = 0
<=> 5x = 0 + 4 hoặc 4x = 0 - 6
<=> 5x = 4 hoặc 4x = -6
<=> x = 4/5 hoặc x = -6/4 = -3/2
b) (x - 5)(3 - 2x)(3x + 4) = 0
<=> x - 5 = 0 hoặc 3 - 2x = 0 hoặc 3x + 4 = 0
<=> x = 0 + 5 hoặc -2x = 0 - 3 hoặc 3x = 0 - 4
<=> x = 5 hoặc -2x = -3 hoặc 3x = -4
<=> x = 5 hoặc x = 3/2 hoặc x = 4/3
c) (2x + 1)(x^2 + 2) = 0
vì x^2 + 2 > 0 nên:
<=> 2x + 1 = 0
<=> 2x = 0 - 1
<=> 2x = -1
<=> x = -1/2
bài 2:
a) (2x + 7)^2 = 9(x + 2)^2
<=> 4x^2 + 28x + 49 = 9x^2 + 36x + 36
<=> 4x^2 + 28x + 49 - 9x^2 - 36x - 36 = 0
<=> -5x^2 - 8x + 13 = 0
<=> (-5x - 13)(x - 1) = 0
<=> 5x + 13 = 0 hoặc x - 1 = 0
<=> 5x = 0 - 13 hoặc x = 0 + 1
<=> 5x = -13 hoặc x = 1
<=> x = -13/5 hoặc x = 1
b) (x^2 - 1)(x + 2)(x - 3) = (x - 1)(x^2 - 4)(x + 5)
<=> x^4 - x^3 - 7x^2 + x + 6 = x^4 + 4x^3 - 9x^2 - 16x + 20
<=> x^4 - x^3 - 7x^2 + x + 6 - x^4 - 4x^3 + 9x^2 + 16x - 20 = 0
<=> -5x^3 - 2x^2 + 17x - 14 = 0
<=> (-x + 1)(x + 2)(5x - 7) = 0
<=> x - 1 = 0 hoặc x + 2 = 0 hoặc 5x - 7 = 0
<=> x = 0 + 1 hoặc x = 0 - 2 hoặc 5x = 0 + 7
<=> x = 1 hoặc x = -2 hoặc 5x = 7
<=> x = 1 hoặc x = -2 hoặc x = 7/5

\(9x^2-1=\left(3x+1\right)\cdot\left(2x-3\right)\\ \Leftrightarrow\left(3x-1\right)\left(3x+1\right)-\left(3x+1\right)\cdot\left(2x-3\right)=0 \\ \Leftrightarrow\left(3x+1\right)\left[\left(3x-1\right)-\left(2x-3\right)\right]=0\\\Leftrightarrow \left(3x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x+1=0\\x+2=0\end{matrix}\right.\Leftrightarrow}\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=-2\end{matrix}\right.\\ \)
1. \(9x^2-1=\left(3x+1\right)\left(2x-3\right)\)
\(\Leftrightarrow\left(3x-1\right)\left(3x+1\right)-\left(3x+1\right)\left(2x-3\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(3x-1-2x+3\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{3}\\x=-2\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{\dfrac{-1}{3};-2\right\}\)
2. \(\left(2x-1\right)^2=49\)
\(\Leftrightarrow\left(2x-1\right)^2-7^2=0\)
\(\Leftrightarrow\left(2x-1-7\right)\left(2x-1+7\right)=0\)
\(\Leftrightarrow\left(2x-8\right)\left(2x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-8=0\\2x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=8\\2x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{4;-3\right\}\)
3. \(\left(5x-3\right)^2-\left(4x-7\right)^2=0\)
\(\Leftrightarrow\left(5x-3-4x+7\right)\left(5x-3+4x-7\right)=0\)
\(\Leftrightarrow\left(x+4\right)\left(9x-10\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\9x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-4\\x=\dfrac{10}{9}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{-4;\dfrac{10}{9}\right\}\)
4. \(\left(2x+7\right)^2=9\left(x+2\right)^2\)
\(\Leftrightarrow4x^2+28x+49=9\left(x^2+4x+4\right)\)
\(\Leftrightarrow4x^2+28x+49=9x^2+36x+36\)
\(\Leftrightarrow\left(4x^2-9x^2\right)+\left(28x-36x\right)=36-49\)
\(\Leftrightarrow-5x^2-8x=-13\)
\(\Leftrightarrow-5x^2-8x+13=0\)
\(\Leftrightarrow-5x^2+5x-13x+13=0\)
\(\Leftrightarrow-5x\left(x-1\right)-13\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x+13\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\5x+13=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-13}{5}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{1;\dfrac{-13}{5}\right\}\)
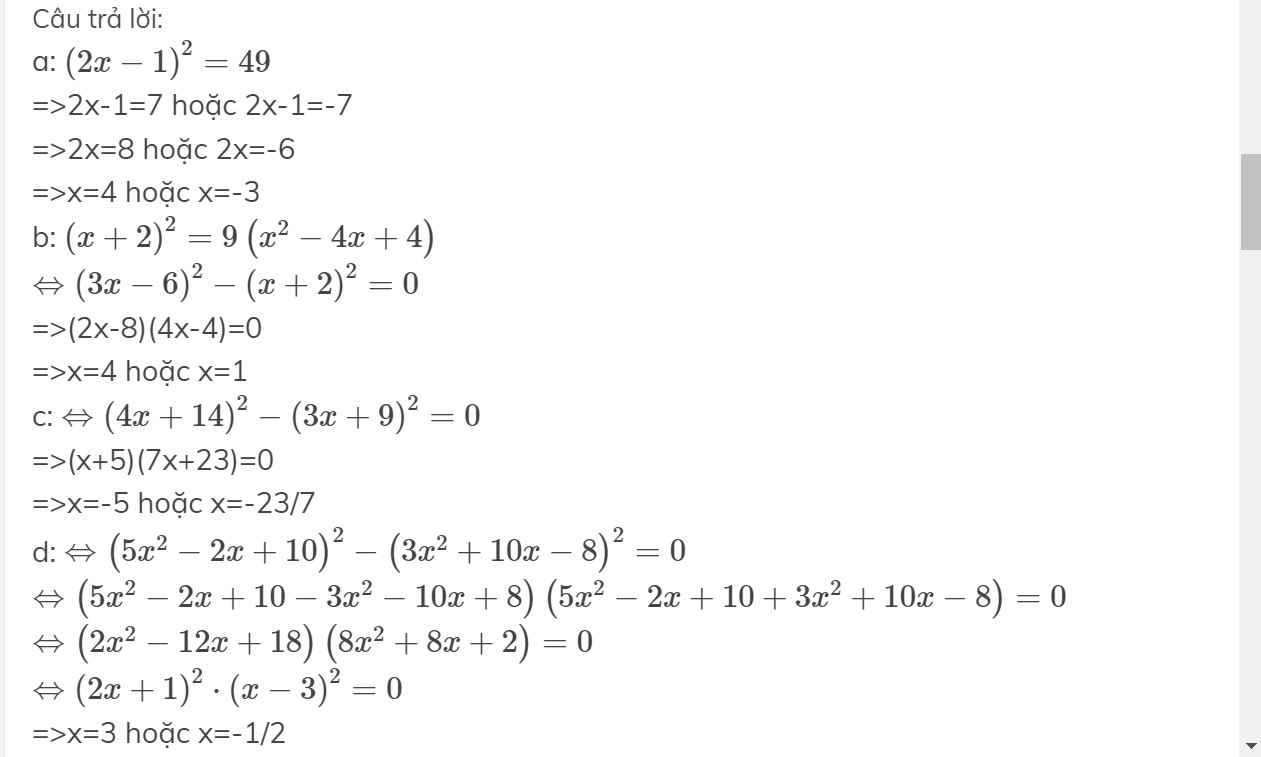
a) \(\left(2x-1\right)^2=49\)
\(\Leftrightarrow\orbr{\begin{cases}2x-1=7\\2x-1=-7\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x=8\\2x=-6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4\\x=-3\end{cases}}\)
jup mk mấy câu kia vs