
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có y3y3=(x−2)4(x−2)4-x4x4=-8(x-1)(x2x2-2x+2)
⇒⇒ y chẵn ⇒⇒ đặt y=-2k(k ϵϵ Z).
⇒⇒ -8k3k3=-8(x-1)(x2x2-2x+2) ⇔⇔ k3k3=(x-1)(x2x2-2x+2)
Do ƯCLN(x-1,x2x2-2x+2)=1 nên x-1=a3a3 và x2x2-2x+2=b3b3 (a,b ϵϵ Z)
Ta có (a3)2(a3)2+1=b3b3 ⇒⇒ b>0. Đặt a2a2=c(c ϵϵ N)
ta có c3c3+1=b3b3 mà b,c ϵϵ N nên b>c.
Th1: b-c ⩾⩾ 2 ⇒⇒ b3b3 ⩾⩾ (c+2)3(c+2)3=c3c3+6c2c2+12c+8>c3c3+1
⇒⇒ trường hợp này loại
Th2:b-c=1 ⇒⇒ c3c3+1=(c+1)3(c+1)3 ⇔⇔ 3c2c2+3c=0
⇔⇔ 3c(c+1)=0 ⇒⇒ c=0( vì c ϵϵ N)
⇒⇒ a=0 ⇒⇒ x=1 và y=0
Vậy nghiệm nguyên của phương trình là x=1 và y=0

a) x + 2x2 - 3x3 + 4x4 - 5 < 2x2 - 3x3 + 4x4 - 6
⇔ x < 2x2 - 3x3 + 4x4 - 6 - 2x2 + 3x3 - 4x4 + 5 (chuyển vế - đổi dấu)
⇔ x < -1 (*)
Vì -2 < -1 nên -2 là nghiệm của bất phương trình
Vậy x = -2 là nghiệm của bất phương trình.
b) (-0,001)x > 0,003
⇔ x < -3 (chia cả hai vế cho -0,001)
Vì -2 > -3 nên -2 không phải nghiệm của bất phương trình
Vậy x = -2 không là nghiệm của bất phương trình.

a) Thay x = -1 vào VT và VP của PT ta được VT = -2 và VP = 1. Vì VT ≠ VP nên x = -1 không là nghiệm của PT đã cho.
b) Tương tự, vì VT = VP = -2 nên t = -1 là nghiệm của PT đã cho.

1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
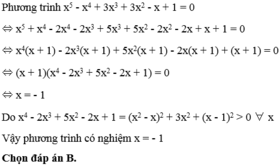

→Xét x ≥ 1 thì:
x⁶ + 3x³ + 1 > x⁶ + 2x³ + 1 = (x³ + 1)²
và x⁶ + 3x³ + 1 < x⁶ + 4x³ + 4 = (x³ + 2)²
=> (x³ + 1)² < y⁴ = x⁶ + 3x³ + 1 < (x³ + 2)²
=> y⁴ nằm giữa 2 số chính phương liên tiếp
=> pt đã cho vô nghiệm với x ≥ 1
→Xét x = 0: tính được y = ± 1 => pt có 2 nº (0; -1) và (0;1)
→Xét x = -1: y⁴ = -1 (vô nº)
→Xét x ≤ -2: để dễ nhìn đặt z = -x => z ≥ 2
pt trở thành: y⁴ = z⁶ - 3z³ + 1
Ta thấy: z⁶ - 3z³ + 1 < z⁶ - 2z³ + 1 (vì z ≥ 2)
=> z⁶ - 3z³ + 1 < (z³ - 1)²
và (z⁶ - 3z³ + 1) - (z⁶ - 4z³ + 4) = z³ - 3 > 0 (do z³ ≥ 8)
=> z⁶ - 3z³ + 1 > z⁶ - 4z³ + 4 = (z³ - 2)²
Do đó: (z³ - 2)² < y⁴ = z⁶ - 3z³ + 1 < (z³ - 1)²
=> y⁴ nằm giữa 2 số chính phương liên tiếp
=> pt đã cho vô nº với x ≤ -2
Kết luận pt đã cho có 2 nº là (0; -1) và (0;1)
→Xét x ≥ 1 thì: x⁶ + 3x³ + 1 > x⁶ + 2x³ + 1 = (x³ + 1)² và x⁶ + 3x³ + 1 < x⁶ + 4x³ + 4 = (x³ + 2)² => (x³ + 1)² < y⁴ = x⁶ + 3x³ + 1 < (x³ + 2)² => y⁴ nằm giữa 2 số chính phương liên tiếp => pt đã cho vô nghiệm với x ≥ 1 →Xét x = 0: tính được y = ± 1 => pt có 2 nº (0; -1) và (0;1) →Xét x = -1: y⁴ = -1 (vô nº) →Xét x ≤ -2: để dễ nhìn đặt z = -x => z ≥ 2 pt trở thành: y⁴ = z⁶ - 3z³ + 1 Ta thấy: z⁶ - 3z³ + 1 < z⁶ - 2z³ + 1 (vì z ≥ 2) => z⁶ - 3z³ + 1 < (z³ - 1)² và (z⁶ - 3z³ + 1) - (z⁶ - 4z³ + 4) = z³ - 3 > 0 (do z³ ≥ 8) => z⁶ - 3z³ + 1 > z⁶ - 4z³ + 4 = (z³ - 2)² Do đó: (z³ - 2)² < y⁴ = z⁶ - 3z³ + 1 < (z³ - 1)² => y⁴ nằm giữa 2 số chính phương liên tiếp => pt đã cho vô nº với x ≤ -2 Kết luận pt đã cho có 2 nº là (0; -1) và (0;1)