KC
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
XO
1 tháng 1 2022
x3 + y3 + 1 = 6xy
<=> (x + y)3 - 3xy(x + y) + 1 = 6xy
<=> (x + y)3 + 8 - 3xy(x + y + 2) = 7
<=> (x + y + 2)(x2 - xy + y2 + 2x + 2y + 4) = 7
Đến đây bạn tự giải tiếp
HH
1
XO
17 tháng 4 2022
x3 - 6xy + y3 = 8
<=> (x + y)3 - 3xy(x + y) - 6xy + 8 = 16
<=> (x + y + 2)(x2 + y2 - xy - 2x - 2y + 4) = 16
<=> \(\left(x+y+2\right)\left[\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\right]=16\)
Nhận thấy \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\ge0\)
=> x + y + 2 > 0
Khi đó 16 = 1.16 = 2.8 = 4.4
Lập bảng
| x + y + 2 | 1 | 16 | 4 | 2 | 8 | |
| \(\left(x-\dfrac{1}{2}y-1\right)^2+3\left(\dfrac{1}{2}y-1\right)^2\) | 16 | 1 | 4 | 8 | 2 | |
| x | ||||||
| y | | |
Đến đó bạn thế x qua y rồi làm tiếp nha
21 tháng 9 2021
Tham khảo: https://vi.wikipedia.org/wiki/%C4%90%E1%BB%8Bnh_l%C3%BD_l%E1%BB%9Bn_Fermat
PT
1
CM
16 tháng 10 2019
x 3 + 4 y = y 3 + 16 x 1 + y 2 = 5 ( 1 + x 2 ) ( 1 )
– Xét x = 0, hệ (I) trở thành 4 y = y 3 y 2 = 4 < = > y = ± 2
– Xét x ≠ 0, đặt y x = t < = > y = x t . Hệ (I) trở thành
x 3 + 4 x t = x 3 t 3 + 16 x 1 + x 2 t 2 = 5 ( 1 + x 2 ) < = > x 3 ( t 3 − 1 ) = 4 x t − 16 x x 2 ( t 2 − 5 ) = 4 < = > x 3 ( t 3 − 1 ) = 4 x ( t − 4 ) ( 1 ) 4 = x 2 ( t 2 − 5 ) ( 2 )
Nhân từng vế của (1) và (2), ta được phương trình hệ quả
4 x 3 ( t 3 − 1 ) = 4 x 3 ( t − 4 ) ( t 2 − 5 ) < = > t 3 − 1 = t 3 − 4 t 2 − 5 t + 20 (Do x ≠ 0) <=>4t 2 + 5 t − 21 = 0 < = > t = − 3 t = 7 4
+ Với t = – 3, thay vào (2) được x2 = 1 ⇔ x = ±1.
x = 1 thì y = –3, thử lại (1;–3) là một nghiệm của (I)
x = –1 thì y = 3, thử lại (–1;3) là một nghiệm của (I)
+ Với t = 7/4 , thay vào (2) được x 2 = − 64 31 (loại)
Vậy hệ (I) có các nghiệm (0;2), (0;–2), (1;–3), (–1;3).
PT
1
CM
16 tháng 2 2017
Ta có: x 3 + y 3 = ( x + y ) 2 < = > ( x + y ) ( x 2 − x y + y 2 − x − y ) = 0
Vì x, y nguyên dương nên x+y > 0, ta có: x 2 − x y + y 2 − x − y = 0
⇔ 2 ( x 2 − x y + y 2 − x − y ) = 0 ⇔ x - y 2 + x - 1 2 + ( y - 1 ) 2 = 2
Vì x, y nguyên nên có 3 trường hợp:
+ Trường hợp 1: x − y = 0 x - 1 2 = 1 ⇔ x = y = 2 , z = 4 y - 1 2 = 1
+ Trường hợp 2: x − 1 = 0 x - y 2 = 1 ⇔ x = 1 , y = 2 , z = 3 y - 1 2 = 1
+ Trường hợp 3: y − 1 = 0 x - y 2 = 1 x - 1 2 = 1 ⇔ x = 2 , y = 1 , z = 3
Vậy hệ có 3 nghiệm (1,2,3);(2,1,3);(2,2,4)
CM
12 tháng 10 2017
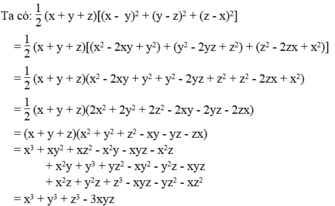
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
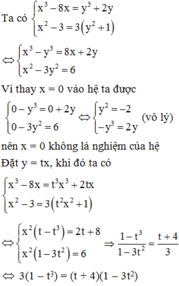
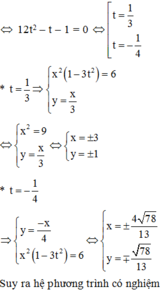
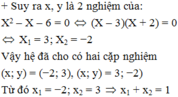
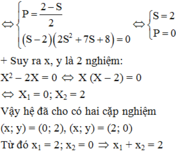
Cái này em thử nhá :33
Giả sử \(x\ge y\ge z\left(x,y,z\inℤ\right)\)
+) Xét TH : \(x=y=z\) Khi đó pt có dạng :
\(x^3+x^3+x^3=2021^{2002}\)
\(\Leftrightarrow3x^3=2021^{2002}\)
\(\Leftrightarrow x^3=\left(2021^{667}\right)^3\)
\(\Leftrightarrow x=2021^{667}\)
Do vậy : \(x=y=z=2021^{667}\)
+) Xét \(x>y>z\) ( Cái này chưa nghĩ :33 )
Đạt ơi cô chưa hiểu chỗ:
\(x^3=\left(2021^{667}\right)^3\)