K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
27 tháng 12 2021
\(\sqrt{x+1}-4x^2=\sqrt{3x}-1\left(x\ge0\right)\left(1\right)\)
\(\Leftrightarrow-4x^2+1+\sqrt{x+1}-\dfrac{\sqrt{6}}{2}=\sqrt{3x}-\dfrac{\sqrt{6}}{2}\)
\(\Leftrightarrow-\left(2x-1\right)\left(2x+1\right)+\dfrac{x+1-\dfrac{3}{2}}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}=\dfrac{3x-\dfrac{3}{2}}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}\)
\(\Leftrightarrow-4\left(x-\dfrac{1}{2}\right)\left(x+\dfrac{1}{2}\right)+\dfrac{x-\dfrac{1}{2}}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3\left(x-\dfrac{1}{2}\right)}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}=0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)\left[-4\left(x+\dfrac{1}{2}\right)+\dfrac{1}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\left(tm\right)\\-4\left(x+\dfrac{1}{2}\right)+\dfrac{1}{\sqrt{x+1}+\dfrac{\sqrt{6}}{2}}-\dfrac{3}{\sqrt{3x}+\dfrac{\sqrt{6}}{2}}=0\left(2\right)\end{matrix}\right.\)
\(\left(x\ge0\right)\Rightarrow\left(2\right)< 0\Rightarrow\left(2\right)vô\) \(nghiệm\)
\(\Rightarrow S=\left\{\dfrac{1}{2}\right\}\)
\(\)
N
2
NH
11 tháng 7 2023
a)
\(x^2-4\sqrt{15}x+19=0\\ < =>x^2-4\sqrt{15}x+60-41=0\\ < =>\left(x-2\sqrt{15}\right)^2-41=0\\ < =>\left(x-2\sqrt{15}-\sqrt{41}\right)\left(x-2\sqrt{15}+\sqrt{41}\right)=0\\ < =>\left[{}\begin{matrix}x-2\sqrt{15}-\sqrt{41}=0\\x-2\sqrt{15}+\sqrt{41}=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=2\sqrt{15}+\sqrt{41}\\x=2\sqrt{15}-\sqrt{41}\end{matrix}\right.\)
b)
\(4x^2+4\sqrt{5}x+5=0\\ < =>\left(2x+\sqrt{5}\right)^2=0\\ < =>2x+\sqrt{5}=0\\ < =>2x=-\sqrt{5}\\ < =>-\dfrac{\sqrt{5}}{2}\)
11 tháng 7 2023
a: Δ=(4căn 15)^2-4*1*19=164>0
Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x=\dfrac{4\sqrt{5}-2\sqrt{41}}{2}=2\sqrt{5}-\sqrt{41}\\x_2=2\sqrt{5}+\sqrt{41}\end{matrix}\right.\)
b: \(\Leftrightarrow\left(2x\right)^2+2\cdot2x\cdot\sqrt{5}+5=0\)
=>(2x+căn 5)^2=0
=>2x+căn 5=0
=>x=-1/2*căn 5
CM
19 tháng 12 2018
4x2 - 2√3 x = 1 - √3.
⇔ 4x2 - 2√3 x – 1 + √3 = 0
Có a = 4; b’ = -√3; c = -1 + √3;
Δ’ = b'2 – ac = (-√3)2 – 4(-1 + √3) = 7 - 4√3 = 4 – 2.2.√3 + (√3)2 = (2 - √3)2.
Phương trình có hai nghiệm phân biệt:
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
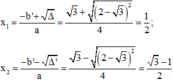
Bài 1: ĐKXĐ: $2\leq x\leq 4$
PT $\Leftrightarrow (\sqrt{x-2}+\sqrt{4-x})^2=2$
$\Leftrightarrow 2+2\sqrt{(x-2)(4-x)}=2$
$\Leftrightarrow (x-2)(4-x)=0$
$\Leftrightarrow x-2=0$ hoặc $4-x=0$
$\Leftrightarrow x=2$ hoặc $x=4$ (tm)
AH
Akai Haruma
Giáo viên
29 tháng 4 2023
Bài 2:
PT $\Leftrightarrow 4x^3(x-1)-3x^2(x-1)+6x(x-1)-4(x-1)=0$
$\Leftrightarrow (x-1)(4x^3-3x^2+6x-4)=0$
$\Leftrightarrow x=1$ hoặc $4x^3-3x^2+6x-4=0$
Với $4x^3-3x^2+6x-4=0(*)$
Đặt $x=t+\frac{1}{4}$ thì pt $(*)$ trở thành:
$4t^3+\frac{21}{4}t-\frac{21}{8}=0$
Đặt $t=m-\frac{7}{16m}$ thì pt trở thành:
$4m^3-\frac{343}{1024m^3}-\frac{21}{8}=0$
$\Leftrightarrow 4096m^6-2688m^3-343=0$
Coi đây là pt bậc 2 ẩn $m^3$ và giải ta thu được \(m=\frac{\sqrt[3]{49}}{4}\) hoặc \(m=\frac{-\sqrt[3]{7}}{4}\)
Khi đó ta thu được \(x=\frac{1}{4}(1-\sqrt[3]{7}+\sqrt[3]{49})\)
LY
1
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
ĐKXĐ: \(x\ge1\)
Do \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{x^2-x^2+1}=1\)
Đặt \(\sqrt{x-\sqrt{x^2-1}}=t\Rightarrow\sqrt{x+\sqrt{x^2-1}}=\dfrac{1}{t}\)
Phương trình trở thành:
\(t+\dfrac{1}{t}=2\Rightarrow t^2-2t+1=0\Rightarrow t=1\)
\(\Rightarrow\sqrt{x-\sqrt{x^2-1}}=1\Leftrightarrow x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x-1=\sqrt{x^2-1}\)
\(\Rightarrow x^2-2x+1=x^2-1\)
\(\Rightarrow x=1\) (thỏa mãn)
CM
4 tháng 11 2017
a) 5 x 2 – x + 2 = 0 ;
a = 5; b = -1; c = 2
Δ = b 2 - 4 a c = ( - 1 ) 2 - 4 . 5 . 2
= 1 - 40 = -39 < 0
Vậy phương trình trên vô nghiệm.
b) 4 x 2 – 4 x + 1 = 0 ;
a = 4; b = -4; c = 1
Δ = b 2 - 4 a c = ( - 4 ) 2 - 4 . 4 . 1 = 16 - 16 = 0
⇒ phương trình có nghiệm kép
x = (-b)/2a = (-(-4))/2.4 = 1/2
Vậy phương trình có nghiệm duy nhất x = 1/2
c) - 3 x 2 + x + 5 = 0
a = -3; b = 1; c = 5
Δ = b 2 - 4 a c = 12 - 4 . ( - 3 ) . 5 = 1 + 60 = 61 > 0
⇒ Do Δ >0 nên áp dụng công thức nghiệm, phương trình có 2 nghiệm phân biệt
x 1 = ( 1 - √ 61 ) / 6 ; x 2 = ( 1 + √ 61 ) / 6
E
1
6 tháng 9 2021
\(\sqrt{x+2\sqrt{x}+1}-\sqrt{x-2\sqrt{x}+1}=2\left(x\ge0\right)\\ \Leftrightarrow\sqrt{\left(\sqrt{x}+1\right)^2}-\sqrt{\left(\sqrt{x}-1\right)^2}=2\\ \Leftrightarrow\sqrt{x}+1-\left|\sqrt{x}-1\right|=2\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}+1-\left(\sqrt{x}-1\right)=2,\forall\sqrt{x}-1\ge0\\\sqrt{x}+1-\left(1-\sqrt{x}\right)=2,\forall\sqrt{x}-1< 0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}0\sqrt{x}=0,\forall x\ge1\\\sqrt{x}=1,\forall x< 1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x\in R,x\ge1\\x=1,x< 1\left(loại\right)\end{matrix}\right.\\ \Leftrightarrow x\in R,x\ge1\)
CM
28 tháng 1 2017
ĐK: y ≥ 1 3 x + 2 y ≥ 1 ⇔ x ≥ 1 − 2 y y ≥ 1 3
Xét 3 y − 1 + x + 2 y − 1 = 0 ⇔ x = y = 1 3
Thay vào (2) không thỏa mãn
Xét 3 y − 1 + x + 2 y − 1 ≠ 0 ⇔ x ≠ 1 3 y ≠ 1 3
(1) ⇔ y ( x – y ) = y − x 3 y − 1 + x + 2 y − 1
Với x = y, thay vào (2) ta được:
x 4 – 4 x 3 + 7 x 2 − 6 x + 2 = 0 ⇔ ( x – 1 ) 2 ( x 2 – 2 x + 2 ) = 0 ⇔ x = 1
Khi đó: y = 1 (TM). Vậy nghiệm của hệ là (1; 1)
Nên x. y = 1
Đáp án:B
ĐKXĐ: x>=-1
\(4x^2-2\sqrt{x+1}=x+2\)
=>\(4x^2-2\sqrt{x+1}-x-2=0\)
=>\(4x^2+3x-4x-3+1-2\sqrt{x+1}=0\)
=>\(\left(4x+3\right)\left(x-1\right)+1-\sqrt{4x+4}=0\)
=>\(\left(4x+3\right)\left(x-1\right)+\dfrac{1-4x-4}{1+\sqrt{4x+4}}=0\)
=>\(\left(4x+3\right)\left(x-1\right)-\dfrac{4x+3}{1+\sqrt{4x+4}}=0\)
=>\(\left(4x+3\right)\left(x-1-\dfrac{1}{1+\sqrt{4x+4}}\right)=0\)
=>4x+3=0
=>x=-3/4(nhận)