K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
1 tháng 3 2022
Câu 3:
Gọi thời gian hai vòi 1 và 2 chảy một mình đầy bể lần lượt là x,y
Trong 1 giờ, vòi 1 chảy được: 1/x(bể)
Trong 1 giờ, vòi 2 chảy được: 1/y(bể)
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{2}{3}\\\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{15}\\\dfrac{1}{x}=\dfrac{1}{5}-\dfrac{1}{15}=\dfrac{2}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{15}{2}\\y=15\end{matrix}\right.\)
10 tháng 11 2021
\(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ Q=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{\left(\sqrt{x}+1\right)^2}{x}\)
LL
4 tháng 6 2021
gọi x là vận tốc của ô tô
y là vận tốc của xe máy (km/h) (x>y>0)
sau 4h 2 xe gặp nhau nên tổng quãng đường AB bằng:
AB= 4.x+4.y = 4.(x+y) (km)
nên thgian ô tô và xe máy đi hết AB lần lượt là:
\(\dfrac{4\left(x+y\right)}{y}\)(h); \(\dfrac{4\left(x+y\right)}{x}\) (h)
vì ô tô đến sớm hơn xe máy 6h nên ta có pt:
\(\dfrac{4\left(x+y\right)}{y}\)-\(\dfrac{4\left(x+y\right)}{x}\)=6
⇔\(\dfrac{4x+4y}{y}\)-\(\dfrac{4x+4y}{x}\)=6
⇔4.\(\dfrac{x}{y}\) +4-4-\(\dfrac{4y}{x}\)=6
⇔\(\dfrac{x}{y}\)-\(\dfrac{y}{x}\)=\(\dfrac{6}{4}\)=\(\dfrac{3}{2}\)
đặt: t=\(\dfrac{x}{y}\) (t>0)
⇒t-\(\dfrac{1}{t}\)=\(\dfrac{3}{2}\)
⇔t2-\(\dfrac{3}{2}\)t-1=0
⇔(t -2)(t +\(\dfrac{1}{2}\))=0
⇔t=2
⇒\(\dfrac{x}{y}\)=2 ⇒x=2y
⇒AB=4.(x+y)=6x=12y
nên thgian ô tô và xe máy đi hết AB lần lượt là:
\(\dfrac{6x}{x}=6\) (h)\(\dfrac{12y}{y}=12\) (h)
5 tháng 6 2021
Gọi thời gian xe máy đi hết quãng đường AB là x (h) (x>4)
thời gian xe máy đi hết quãng đường AB là y (h) (y>4)
Trong 1 giờ xe máy đi được \(\dfrac{1}{x}\) (quãng đường)
Trong 1 giờ ô tô đi được \(\dfrac{1}{y}\) (quãng đường)
Trong 1 giờ hai xe đi được \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\left(1\right)\)
Mà thời gian ô tô về đến A sớm hơn xe máy về đến B là 6 giờ nên: \(x-y=6\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{4}\\x-y=6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{x-6}=\dfrac{1}{4}\\y=x-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-14x+24=0\\y=2-6\end{matrix}\right.\)(ĐK:\(x\ne6\)) \(\Leftrightarrow\left\{{}\begin{matrix}x=12\\y=6\end{matrix}\right.\)(TM)
Vậy thời gian xe máy đi hết quãng đường AB là 12 giờ
thời gian ô tô đi hết quãng đường AB là 6giờ
-Chúc bạn học tốt-
28 tháng 5 2022
Câu 2:
Ta có: \(x^3+3x^2-4x-12=0\)
\(\Leftrightarrow x^2\left(x+3\right)-4\left(x+3\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x^2-4\right)=0\)
\(\Leftrightarrow\left(x+3\right)\left(x-2\right)\left(x+2\right)=0\)
hay \(x\in\left\{-3;2;-2\right\}\)
23 tháng 5 2023
b: x1^2+m(x2)=13
=>x1^2+x2(x1+x2)=13
=>(x1+x2)^2-x1x2=13
=>m^2-m+1-13=0
=>m^2-m-12=0
=>m=4; m=-3
!
HP
1 tháng 9 2021
10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
HP
1 tháng 9 2021
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)
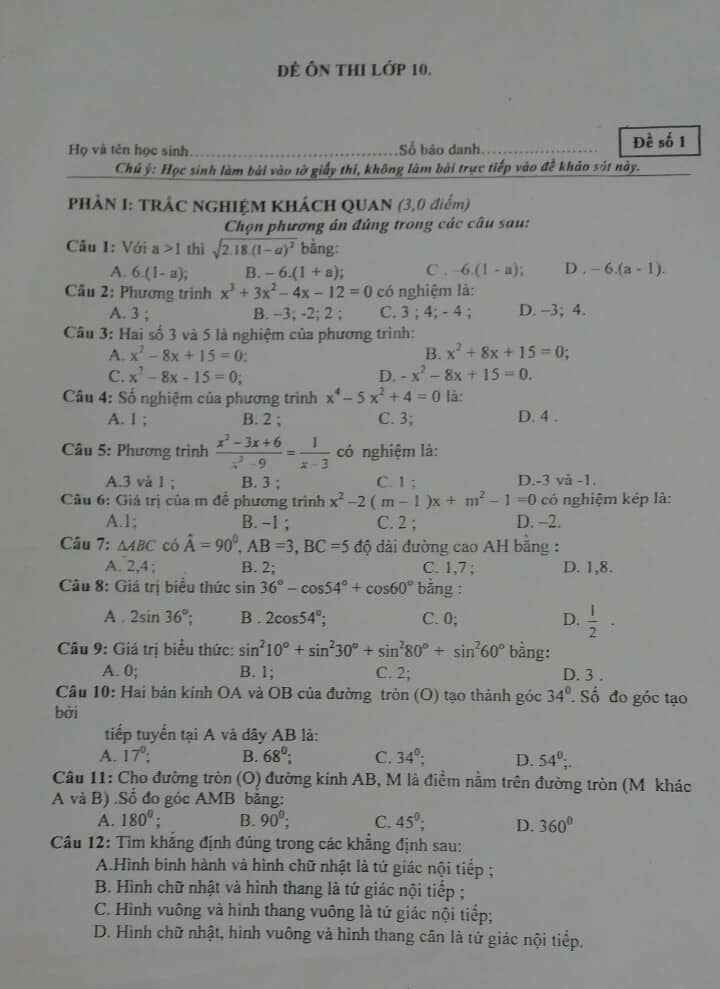
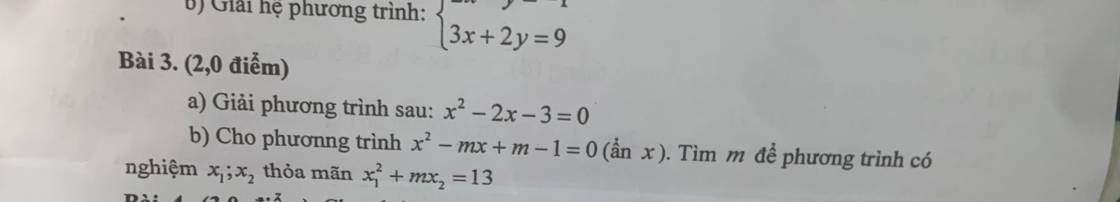
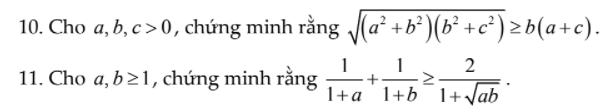hình như là đề vio lớp 9 vòng 17 năm ngoái