K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 11 2016
GTNN (A)=3178+2017 khi x=0 ko co GTLN
GTLN(b)=2017 khi x=-3 va y=5 khong co GTNN
GTNN(c)=2018 khi x=-1 va y=5 khong co GTLN
neu can giai thich thi h
ko thi thoi
10 tháng 11 2016
em cũng muốn làm phước giúp chị lắm chứ nhưng em mới ở lớp 6 thui
NY
3
28 tháng 1 2023
Từ bài toán, ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}\) và \(a+b+c=24\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{a}{3}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{3+4+5}=\dfrac{24}{12}=2\)
Suy ra:
\(a=2\cdot3=6\)
\(b=2\cdot4=8\)
\(c=3\cdot5=15\)
XO
1 tháng 8 2021
Ta có \(5x=3y\Rightarrow\frac{x}{3}=\frac{y}{5}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{x-y}{3-5}=\frac{10}{-2}=-5\)
\(\Rightarrow x=3.\left(-5\right)=-15;y=\left(-5\right).5=-25\)
Vậy x = -15 ; y = -25
25 tháng 10 2018
Gọi số học sinh lần lượt là x, y, z của các khối 6,7,8
Theo đề ra, ta có :
x/10=y/9=z/8 và x-z = 50
=> x/10=y/9=z/8= x-z/10-8= 50/2= 25
=>x= 10.25= 250
=>y=9.25=225
=>z=8.25=200
Vậy số học sinh 3 khối 6,7,8, lần lượt là 250, 225, 200
Bị sai đề đó ! nên mình sửa lại
22 tháng 7 2023
a: góc yOz=180-60=120 độ
góc zOm=góc yOm=120/2=60 độ
b: góc xOn=góc zOm=60 độ
=>góc xOn=góc xOy
=>Ox là phân giác của góc yOn
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
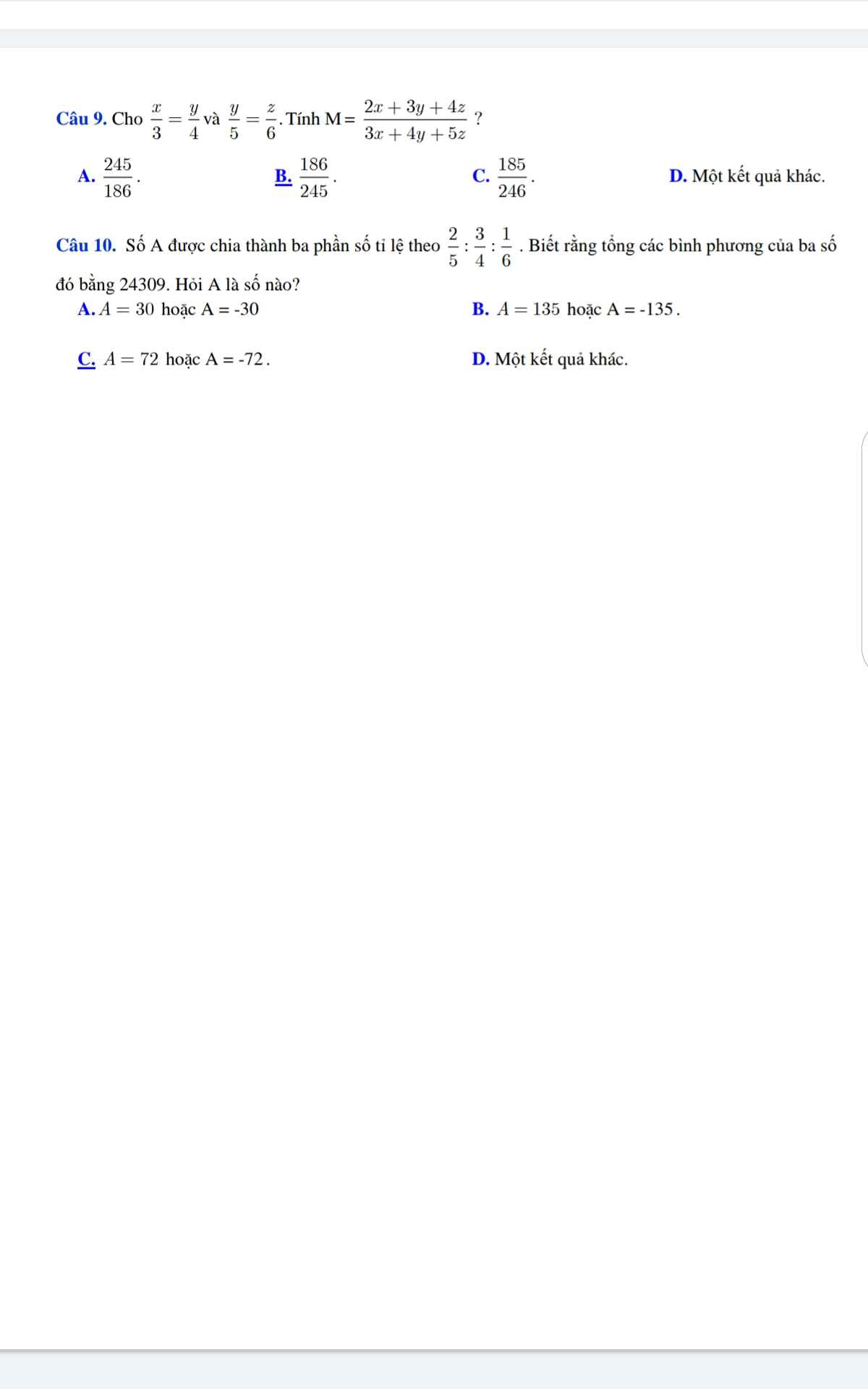
Câu 9 cần bs điều kiện $x,y,z\neq 0$
$\frac{x}{3}=\frac{y}{4}\Rightarrow \frac{x}{15}=\frac{y}{20}$
$\frac{y}{5}=\frac{z}{6}\Rightarrow \frac{y}{20}=\frac{z}{24}$
$\Rightarrow \frac{x}{15}=\frac{y}{20}=\frac{z}{24}$ và đặt $=t$ (đk: $t\neq 0$)
$\Rightarrow x=15t; y=20t; z=24t$
Khi đó:
$M=\frac{2.15t+3.20t+4.24t}{3.15t+4.20t+5.24t}=\frac{186t}{245t}=\frac{186}{245}$
Đáp án B.
AH
Akai Haruma
Giáo viên
15 tháng 10 2021
Câu 10:
Giả sử số $A$ được chia thành 3 phần $a,b,c$ sao cho
$a:b:c=\frac{2}{5}: \frac{3}{4}: \frac{1}{6}$
Đặt $a=\frac{2}{5}t; b=\frac{3}{4}t; c=\frac{1}{6}t$
$A=a+b+c=\frac{2}{5}t+\frac{3}{4}t+\frac{1}{6}t=\frac{79}{60}t$
Có:
$a^2+b^2+c^2=(\frac{2}{5}t)^2+(\frac{3}{4}t)^2+(\frac{1}{6}t)^2=24309$
$t^2=32400$
$t=\pm 180$
$\Rightarrow A=\frac{79}{60}t=\frac{79}{60}\pm 180=\pm 237$
Đáp án D.
\(a,\left\{{}\begin{matrix}AC=AD\\\widehat{ACE}=\widehat{DCE}\left(CE.là.p/g\right)\\CE.chung\end{matrix}\right.\Rightarrow\Delta ACE=\Delta DCE\left(c.g.c\right)\\ \Rightarrow AE=ED\\ b,\Delta ACE=\Delta DCE\Rightarrow\widehat{BAC}=\widehat{CED}=90^0\\ \Rightarrow BC\perp DE\\ \Rightarrow\widehat{BED}+\widehat{B}=90^0\)
Mà \(\widehat{ACB}+\widehat{B}=90^0\left(\Delta ABC\perp A\right)\)
Vậy \(\widehat{BED}=\widehat{ACB}\)
\(c,\) Gọi giao của phân giác \(\widehat{BED}\) và BC là F
\(\Rightarrow\widehat{FED}=\dfrac{1}{2}\widehat{BED}\)
Lại có \(\Delta ACE=\Delta DCE\Rightarrow\widehat{AEC}=\widehat{CED}\)
Mà \(\widehat{AEC}+\widehat{CED}=\widehat{AED}\Rightarrow\widehat{CED}=\dfrac{1}{2}\widehat{AED}\)
Ta có \(\widehat{CEF}=\widehat{CED}+\widehat{FED}=\dfrac{1}{2}\left(\widehat{AED}+\widehat{DEB}\right)\)
Mà \(\widehat{AED}+\widehat{DEB}=180^0\)
Do đó \(\widehat{CEF}=90^0\Rightarrow CE\perp EF\)
Suy ra cái đề
Anh chăm chỉ thế