K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NA
0
V
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm
YN
2
22 tháng 9 2021
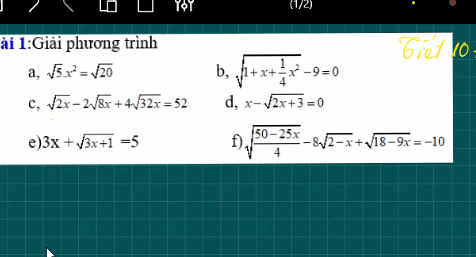
a) \(\Leftrightarrow x^2=\sqrt{4}\)
\(\Leftrightarrow x^2=2\Leftrightarrow x=\pm2\)
b) \(\Leftrightarrow\sqrt{\left(\dfrac{1}{2}x+1\right)^2}=9\)
\(\Leftrightarrow\left|\dfrac{1}{2}x+1\right|=9\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+1=9\\\dfrac{1}{2}x+1=-9\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=-16\end{matrix}\right.\)
c) \(\Leftrightarrow\sqrt{2x}-4\sqrt{2x}+16\sqrt{2x}=52\left(đk:x\ge0\right)\)
\(\Leftrightarrow13\sqrt{2x}=52\Leftrightarrow\sqrt{2x}=4\Leftrightarrow2x=16\Leftrightarrow x=8\left(tm\right)\)
22 tháng 9 2021
f: Ta có: \(\sqrt{\dfrac{50-25x}{4}}-8\sqrt{2-x}+\sqrt{18-9x}=-10\)
\(\Leftrightarrow\sqrt{2-x}\cdot\dfrac{5}{2}-8\sqrt{2-x}+3\sqrt{2-x}=-10\)
\(\Leftrightarrow\sqrt{2-x}=4\)
\(\Leftrightarrow2-x=16\)
hay x=-14
6 tháng 10 2021
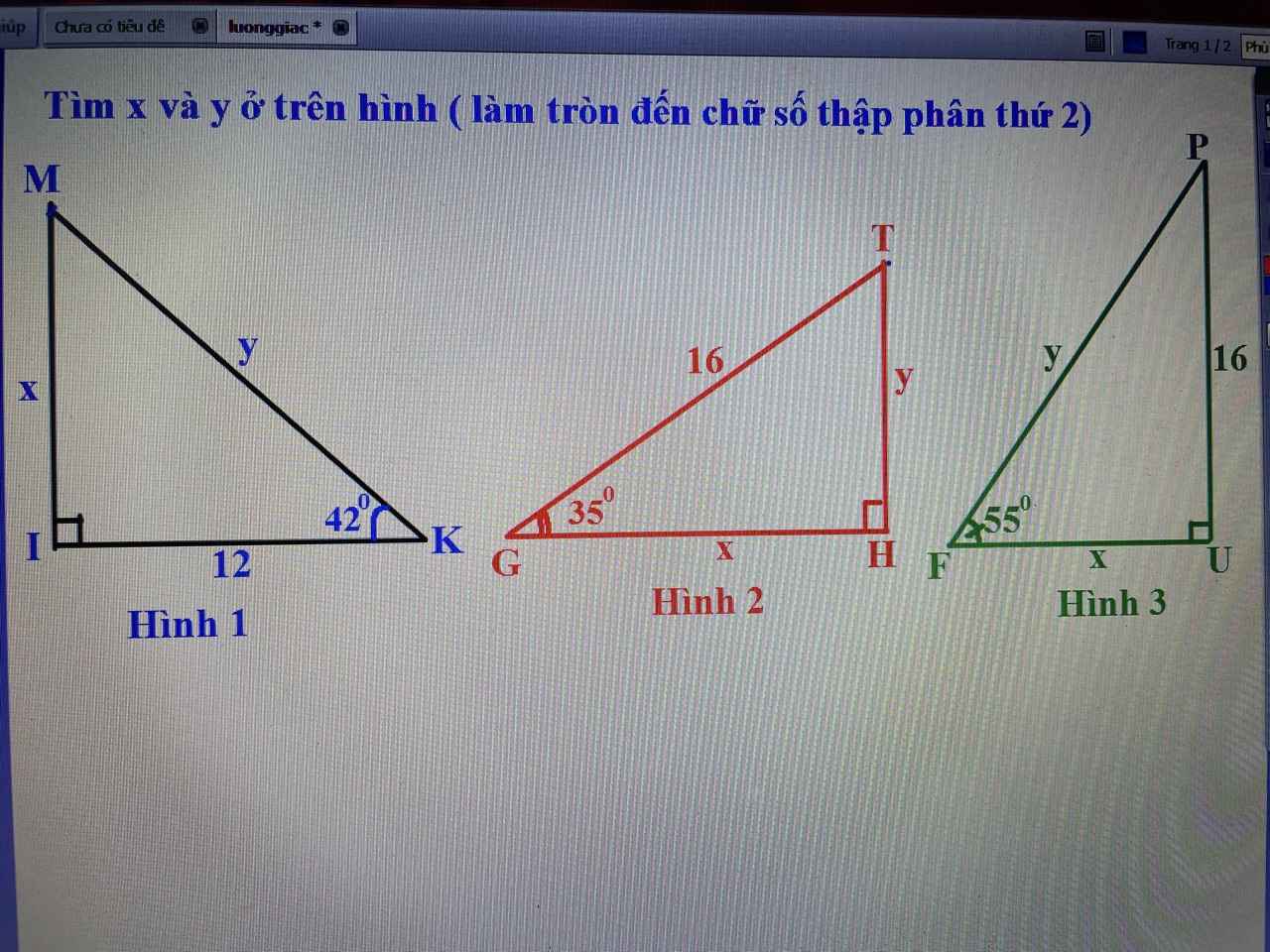
Hình 1:
Áp dụng tslg:
\(cosK=\dfrac{IK}{MK}\)\(\Rightarrow cos42^0=\dfrac{12}{y}\Rightarrow y\approx16,15\)
\(tanK=\dfrac{IM}{IK}\Rightarrow tan42^0=\dfrac{x}{12}\Rightarrow x\approx10,8\)
Hình 2:
\(sinG=\dfrac{HT}{GT}\Rightarrow sin35^0=\dfrac{y}{16}\Rightarrow y\approx9,18\)
\(cosG=\dfrac{GH}{GT}\Rightarrow cos35^0=\dfrac{x}{16}\Rightarrow x\approx10,11\)
6 tháng 10 2021
Hình 1:
\(x=12\cdot\tan42^0\simeq10.8\left(cm\right)\)
\(y=\sqrt{10.8^2+12^2}\simeq16,14\left(cm\right)\)
2 tháng 7 2021
Ta có: \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\left(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{xz}\right)}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\dfrac{x+y+z}{xyz}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)
V
0
30 tháng 11 2021
c: Thay P=-4 vào P, ta được:
\(-\sqrt{x}=-4x-4\sqrt{x}-4\)
\(\Leftrightarrow4x+3\sqrt{x}+4=0\)
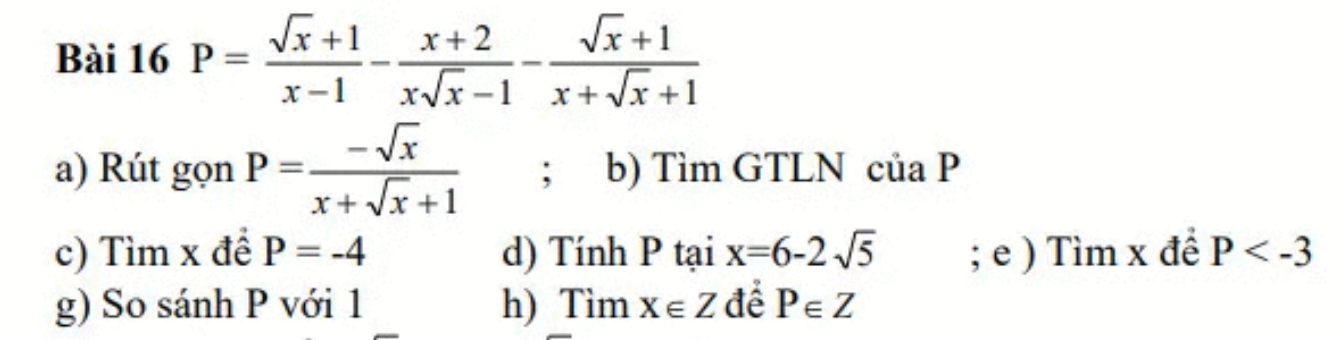
cái đề đâu bn