K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
10 tháng 3 2021
Bài 1:
PT $\frac{1}{x}+1=0\Leftrightarrow x=-1$
PT $x^2+1=0\Leftrightarrow x^2=-1< 0$ (vô lý) nên PT vô nghiệm.
Vậy PT(1) có tập nghiệm $\left\{-1\right\}$ còn PT(2) có tập nghiệm $\left\{\varnothing\right\}$ nên 2 PT này không tương đương.
AH
Akai Haruma
Giáo viên
10 tháng 3 2021
Bài 3:
ĐKXĐ: $x\neq 0;\pm 1$
a)
\(Q=\left(\frac{x^2-1}{2x}\right)^2.\frac{(x-1)^2-(x+1)^2}{(x-1)(x+1)}=\frac{(x-1)^2(x+1)^2}{4x^2}.\frac{-4x}{(x+1)(x-1)}=\frac{-(x-1)(x+1)}{x}=\frac{1-x^2}{x}\)
b) Để $Q=-1,5\Leftrightarrow \frac{1-x^2}{x}=-1,5$
$\Rightarrow 1-x^2=-1,5x$
$\Leftrightarrow x^2-1,5x-1=0$
$\Leftrightarrow (x-2)(x+0,5)=0\Rightarrow x=2$ hoặc $x=-0,5$ (đều thỏa mãn)
c)
Để $Q$ không âm thì $\frac{1-x^2}{x}\geq 0$. Điều này xảy ra khi:
TH1 :\(\left\{\begin{matrix} 1-x^2\geq 0\\ x> 0\end{matrix}\right.\Leftrightarrow 0< x\leq 1\)
TH2: \(\left\{\begin{matrix} 1-x^2\leq 0\\ x<0\end{matrix}\right.\Leftrightarrow x\leq -1\)
Kết hợp với ĐKXĐ suy ra $0< x< 1$ hoặc $x< -1$
HV
2
11 tháng 10 2021
1: Ta có: \(\left(x^3-4x^2\right)-\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=1\\x=-1\end{matrix}\right.\)
NV
0
9 tháng 11 2021
a: Xét ΔABC có
M là trung điểm của BC
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔACB
Suy ra: MN//AB
hay ABMN là hình thang
9 tháng 11 2021
a, Vì M,N là trung điểm BC,AC nên MN là đtb tg ABC
Do đó MN//AB hay ABMN là hthang
b, Vì N là trung điểm AC và MD (t/c đối xứng) nên ADCM là hbh
c, Vì ADCM là hbh nên AD=CM=BM và AD//CM hay AD//BM
Do đó ADMB là hbh
Mà I là trung điểm AM nên cũng là trung điểm BD
Vậy B,I,D thẳng hàng
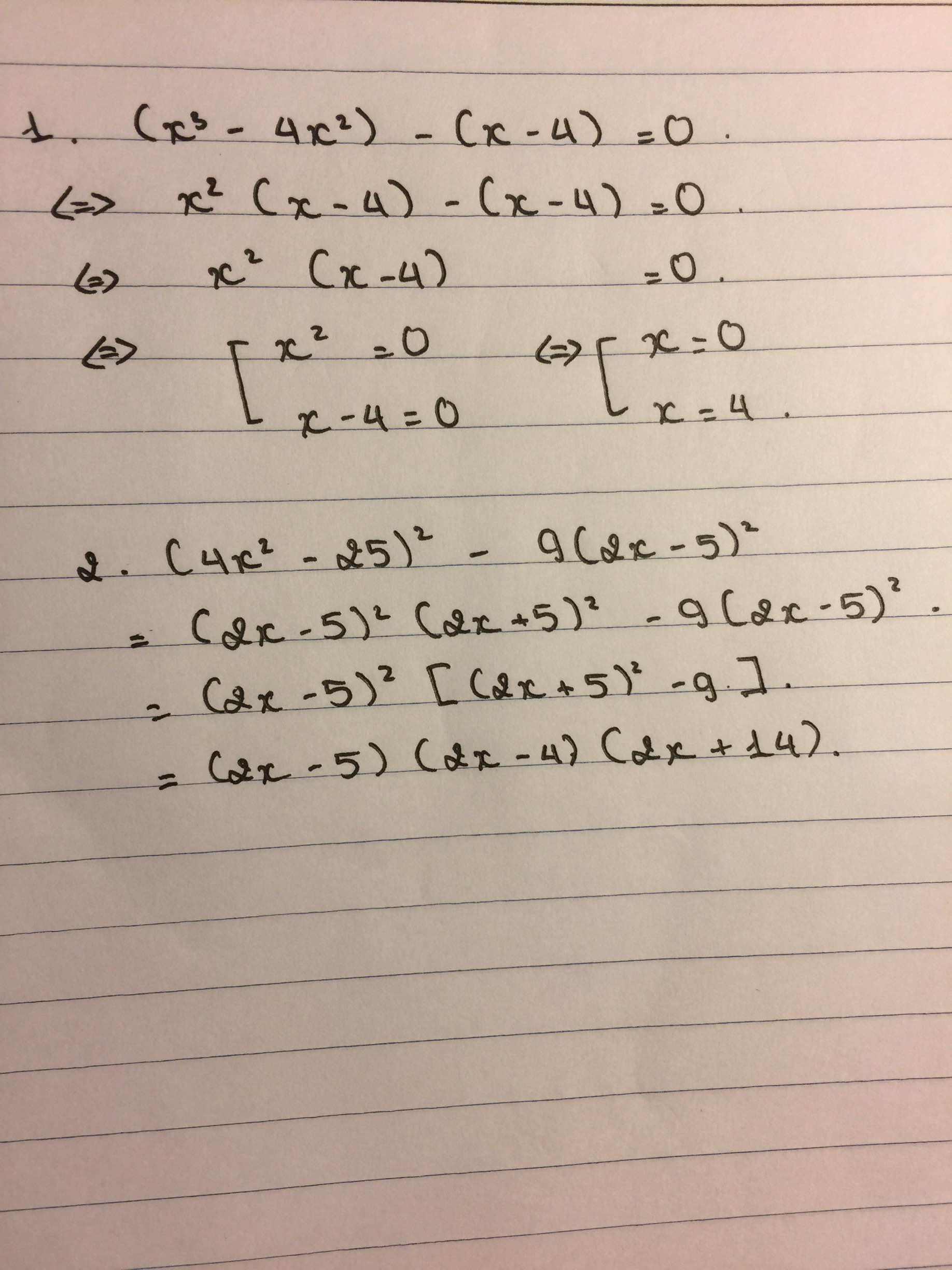
5:
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng vơi ΔHAC
=>AB/HA=BC/AC
=>AB*AC=AH*CB
c: \(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=4/8=0,5
=>AD=1,5cm; CD=2,5cm
BH=3^2/5=1,8cm
=>AH=2,4cm
AE/AB=EH/BH
=>AE/3=EH/1,8=(AE+EH)/(3+1,8)=0,5
=>AE=1,5cm; HE=0,9cm
\(S_{BHE}=\dfrac{1}{2}\cdot1.8\cdot0.9=0.81\left(cm^2\right)\)
\(S_{ABD}=\dfrac{1}{2}\cdot BA\cdot AD=\dfrac{1}{2}\cdot3\cdot1.5=2.25\left(cm^2\right)\)
=>\(\dfrac{S_{BHE}}{S_{ABD}}=\dfrac{81}{225}=\dfrac{9}{25}\)