Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




CTM: \(R_1nt\left(R_2//R_3\right)\)
a)\(R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot25}{20+25}=\dfrac{100}{9}\Omega\)
\(R_{tđ}=R_1+R_{23}=15+\dfrac{100}{9}=\dfrac{235}{9}\Omega\)
b)\(I_1=I=\dfrac{U}{R_{tđ}}=\dfrac{20}{\dfrac{235}{9}}=\dfrac{36}{47}A\)
\(U_{12}=I_{12}\cdot R_{12}=\dfrac{36}{47}\cdot\dfrac{100}{9}=\dfrac{400}{47}V\)
\(I_2=\dfrac{U_2}{R_2}=\dfrac{\dfrac{400}{47}}{20}=\dfrac{20}{47}A;I_3=\dfrac{U_3}{R_3}=\dfrac{\dfrac{400}{47}}{25}=\dfrac{16}{47}A\)

\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)

\(R=\dfrac{U}{I}=\dfrac{12}{0,1}=120\left(\Omega\right)\)
\(R=\rho\dfrac{l}{S}\Rightarrow S=\dfrac{\rho.l}{R}=\dfrac{0,4.10^{-6}.6}{120}=2.10^{-8}\left(m^2\right)\)

Bài 2:
a. \(P=UI\Rightarrow I=\dfrac{P}{U}=\dfrac{528}{220}=2,4\left(A\right)\)
b. \(R=\dfrac{U}{I}=\dfrac{220}{2,4}\approx91,7\left(\Omega\right)\)

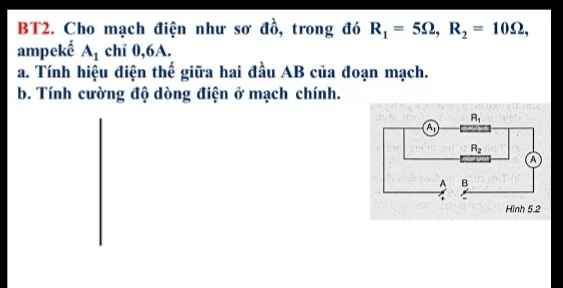
a, HĐT giữa 2 đầu R1:
Ta có: \(I_1=\dfrac{U_1}{R_1}\Leftrightarrow U_1=I_1R_1=0,6.5=3\left(V\right)\)
Mà UAB=U1=U2=3V
b, Điện trở tương đương:
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}=\dfrac{5.10}{5+10}=3,33\left(\Omega\right)\)
CĐDĐ ở mạch chính:
\(I_{AB}=\dfrac{U_{AB}}{R_{tđ}}=\dfrac{3}{3,33}=0,9\left(A\right)\)

a. Bạn tự vẽ sơ đồ mạch điện nhé!
b. \(P=UI\)
\(\Rightarrow\left[{}\begin{matrix}I1=\dfrac{P1}{U1}=\dfrac{440}{220}=2\left(A\right)\\I2=\dfrac{P2}{U2}=\dfrac{110}{220}=0,5\left(A\right)\end{matrix}\right.\)
c. \(\left[{}\begin{matrix}R1=\dfrac{U1}{I1}=\dfrac{220}{2}=110\left(\Omega\right)\\R2=\dfrac{U2}{I2}=\dfrac{220}{0,5}=440\left(\Omega\right)\end{matrix}\right.\)
d. \(A=\left(P1.t\right)+\left(P2.t\right)=\left(440.4.30\right)+\left(110.4.30\right)=66000\left(Wh\right)=66\left(kWh\right)\)
\(\Rightarrow T=A.450=66.450=29700\left(dong\right)\)