K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7 tháng 1 2022
a: Xét ΔAHI và ΔADI có
AH=AD
HI=DI
AI chung
Do đó: ΔAHI=ΔADI
b: Ta có: ΔADH cân tại A
mà AI là đường trung tuyến
nên AI là đường cao
c: Xét ΔHAK và ΔDAK có
AH=AD
\(\widehat{HAK}=\widehat{DAK}\)
AK chung
Do đó: ΔHAK=ΔDAK
Suy ra: \(\widehat{ADK}=\widehat{AHK}=90^0\)
=>DK⊥AC
mà AC⊥AB
nên KD//AB
NN
1
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
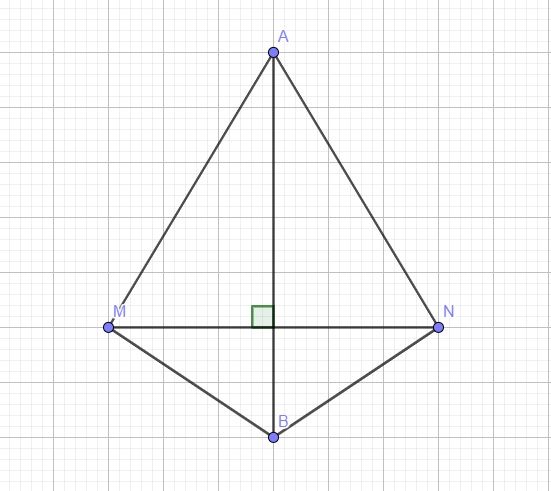
Do A thuộc trung trực đoạn MN nên \(AM=AN\)
Do B thuộc trung trực đoạn MN nên \(BM=BN\)
Xét 2 tam giác MAB và NAB có:
\(\left\{{}\begin{matrix}AM=AN\left(cmt\right)\\BM=BN\left(cmt\right)\\AB\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta MAB=\Delta NAB\left(c.c.c\right)\)
12 tháng 8 2018
Qua B vẽ đường thẳng Bz song song với Ax
Bz // Ax suy ra góc BAx = ABz =30 ( hai góc so le trong)
Bz // Cy suy ra góc BCy = CBz =40
suy ra ABC = ABz + CBz = 30+40 =70 độ
VP
1
BC
1
30 tháng 3 2022
BẠN CÓ THỂ TẢI QANDA VỀ MÁY ĐIỆN THOẠI VÀ TRA HAI CÂU NÀY Ở TRÊN ỨNG DỤNG QANDA LÀ CÓ KẾT QUẢ NGAY. NẾU KO CÓ THÌ BẤM VÀO MỤC HỎI GIA SƯ LÀ SẼ CÓ GIA SƯ GIẢI NGAY CHO BẠN.
AH
Akai Haruma
Giáo viên
21 tháng 12 2022
Lời giải:
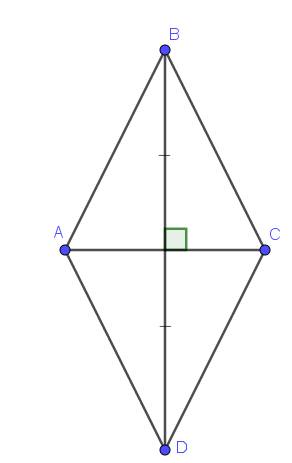
Vì $B,D$ đối xứng với nhau qua $AC$ nên $AC$ chính là trung trực của $BD$
$\Rightarrow AB=AD; CB=CD$. Mà $ABC$ là tam giác cân tại $B$ nên $AB=BC$
$\Rightarrow AB=BC=AD=CD$
Xét tam giác $ABD$ và $CBD$ có:
$AB=CB$ (cmt)
$BD$ chung
$AD=CD$ (cmt)
$\Rightarrow \triangle ABD=\triangle CBD$ (c.c.c)
