K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 4 2022
Câu 4:
Thay x=2 và y=-1 vào hệ, ta được:
\(\left\{{}\begin{matrix}2a-b=4\\2b+2=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\a=1\end{matrix}\right.\)
1 tháng 1 2022
Câu 4:
\(a,\tan B=\dfrac{AC}{AB}=\dfrac{12}{5}\approx\tan67^0\\ \Rightarrow\widehat{B}\approx67^0\\ b,\text{Áp dụng PTG: }BC=\sqrt{AC^2+AB^2}=13\left(cm\right)\\ \text{Áp dụng HTL: }\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{144}{13}\left(cm\right)\\AH=\sqrt{BH\cdot CH}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
14 tháng 4 2021
Gọi vận tốc xe máy là x ( x > 0, km/h )
vận tốc ô tô là x + 10 km/h
Thời gian xe máy đi từ A -> B là : \(\dfrac{100}{x}\)giờ
Thời gian ô tô đi từ A -> B là : \(\dfrac{100}{x+10}\)giờ
Do ô tô và xe máy suất phát cùng lúc, quãng đường AB ko đổi và ô tô đến B trước xe máy 30 phút = 1/2 giờ
nên ta có phương trình : \(\dfrac{100}{x}-\dfrac{100}{x+10}=\dfrac{1}{2}\)
giải phương trình ta thu được : \(x=40\left(chon\right);x=-50\left(loai\right)\)
Vậy vận tốc xe máy là 40 km/h
vận tốc ô tô là 40 + 10 = 50 km/h
14 tháng 4 2021
Câu IV:
Gọi vận tốc của xe máy là x(km/h)(Điều kiện: x>0)
Vận tốc của xe ô tô là: x+10(km/h)
Thời gian xe máy đi từ A đến B là: \(\dfrac{100}{x}\left(h\right)\)
Thời gian ô tô đi từ A đến B là: \(\dfrac{100}{x+10}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{100}{x}-\dfrac{100}{x+10}=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{200\left(x+10\right)}{2x\left(x+10\right)}-\dfrac{200x}{2x\left(x+10\right)}=\dfrac{x\left(x+10\right)}{2x\left(x+10\right)}\)
Suy ra: \(x^2+10x=200x+2000-200x\)
\(\Leftrightarrow x^2+50x-40x-2000=0\)
\(\Leftrightarrow x\left(x+50\right)-40\left(x+50\right)=0\)
\(\Leftrightarrow\left(x+50\right)\left(x-40\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+50=0\\x-40=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-50\left(loại\right)\\x=40\left(nhận\right)\end{matrix}\right.\)
Vậy: Vận tốc của xe máy là 40km/h
Vận tốc của ô tô là 50km/h
NT
3
22 tháng 6 2023
4:
a: góc ADB=1/2*180=90 độ
=>góc ADC=90 độ
góc AHC=góc ADC=90 độ
=>AHDC nội tiếp
b: Xét ΔEBA vuông tại E và ΔHAC vuông tại H có
góc EBA=góc HAC
=>ΔEBA đồng dạng với ΔHAC
=>góc EAB=góc HCA=góc EDB
=>góc EDB=góc ADH
24 tháng 7 2021
18) Ta có: \(H=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}\cdot\left(\sqrt{x}+1\right)-\left(2\sqrt{x}-1\right)\)
\(=x+\sqrt{x}-2\sqrt{x}+1\)
\(=x-\sqrt{x}+1\)
19) Ta có: \(T=\dfrac{a-3\sqrt{a}-4}{\sqrt{a}+1}\)
\(=\dfrac{\left(\sqrt{a}-4\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\sqrt{a}-4\)
TH
1
8 tháng 2 2022
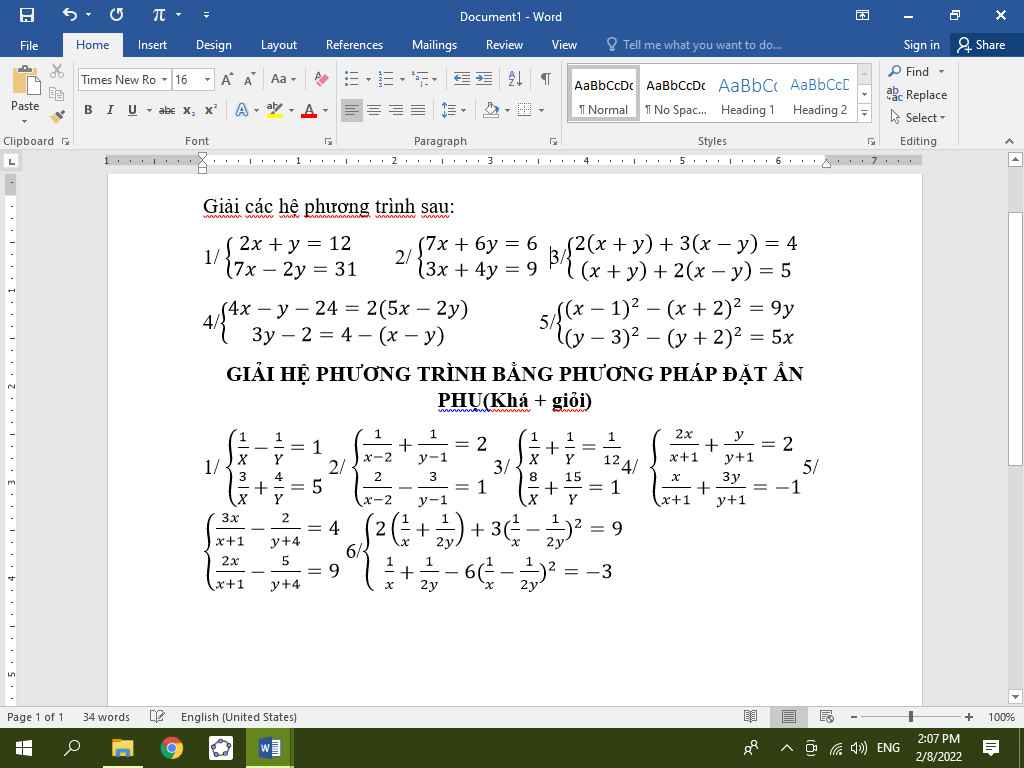
1, \(\left\{{}\begin{matrix}4x+2y=24\\7x-2y=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=55\\y=12-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=2\end{matrix}\right.\)
2, thiếu đề
4, \(\left\{{}\begin{matrix}4x-y-24=10x-4y\\3y-2=4-x+y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-6x+3y=24\\-6x-12y=-36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15y=60\\x=6-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=-2\end{matrix}\right.\)
S
2
4 tháng 12 2021
\(c,B< A\\ \Rightarrow\dfrac{\sqrt{x}+4}{\sqrt{x}-2}< \dfrac{\sqrt{x}+1}{\sqrt{x}-2}\\ \Rightarrow\sqrt{x}+4< \sqrt{x}+1\left(vô.lí\right)\)
Vậy không có x nguyên thỏa mãn đề bài
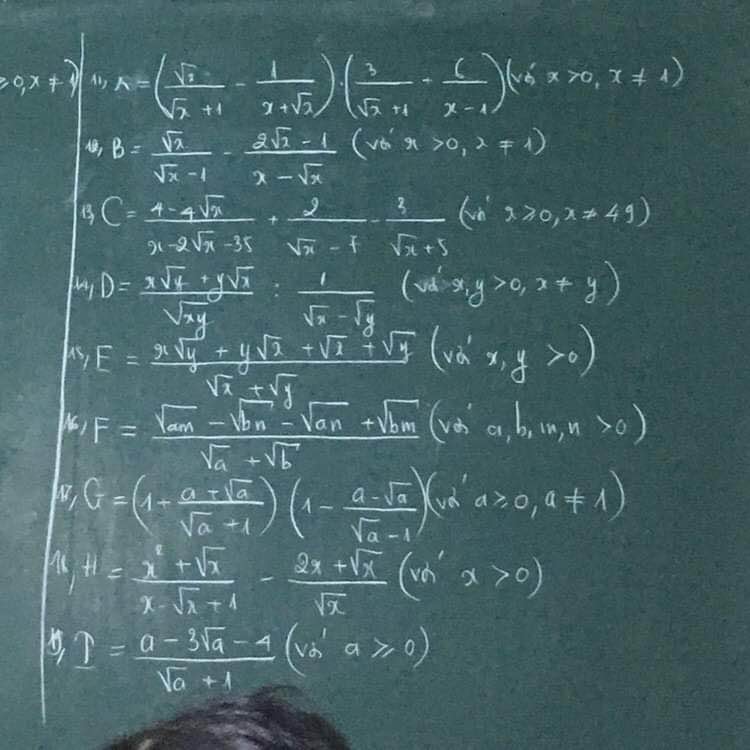
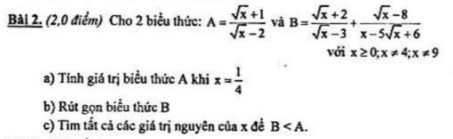
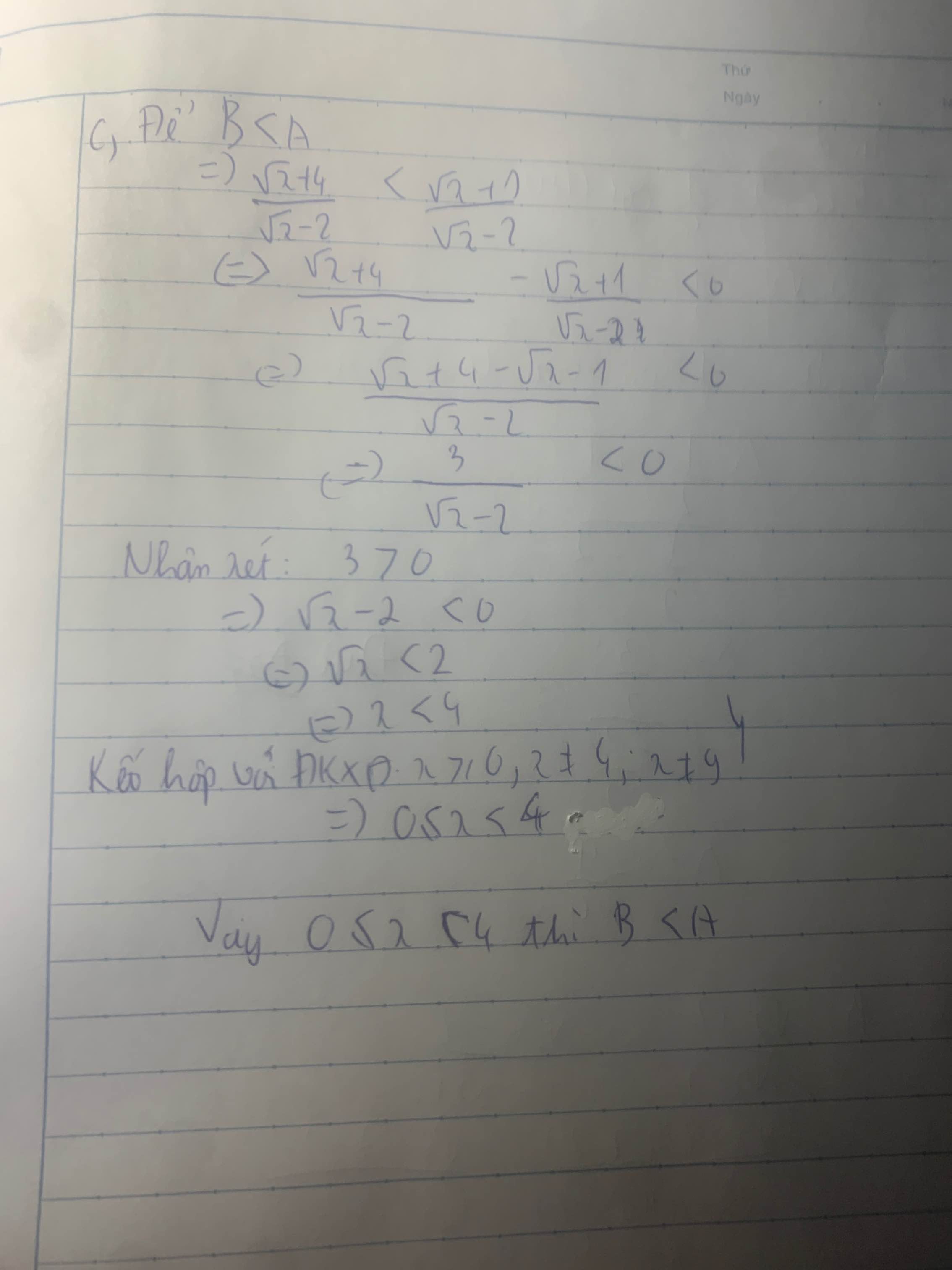
4:
Gọi chiều rộng là x
=>Chiều dài là x+3
Theo đề, ta có: x(x+3)=180
=>x^2+3x-180=0
=>(x+15)(x-12)=0
=>x=-15(loại) hoặc x=12(nhận)
=>Chiều dài là 15cm