K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LH
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
\(a^2+b^2+c^2=1\Rightarrow\left\{{}\begin{matrix}a^2\le1\\b^2\le1\\c^2\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|a\right|\le1\\\left|b\right|\le1\\\left|c\right|\le1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a^3\le a^2\\b^3\le b^2\\c^3\le c^2\end{matrix}\right.\)
\(\Rightarrow a^3+b^3+c^3\le a^2+b^2+c^2=1\)
Đẳng thức xảy ra khi và chỉ khi: \(\left(a;b;c\right)=\left(0;0;1\right)\) và các hoán vị
\(\Rightarrow S=0+0+1=1\)
KL
1
19 tháng 12 2021
a: Xét tứ giác ABDC có
N là trung điểm của BC
N là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
NN
27 tháng 4 2017
Ta xét:
1. Nếu \(x=2015\) hoặc \(x=2016\) thì thỏa mãn đề bài
2. Nếu \(x< 2015\) thì \(\hept{\begin{cases}\left|x-2015\right|^{2015}>0\\\left|x-2016\right|^{2016}>1\end{cases}}\)
\(\Leftrightarrow\left|x-2015\right|^{2015}+\left|x-2016\right|^{2016}>0+1=1\) (vô nghiệm)
3. Nếu \(x>2016\) thì \(\hept{\begin{cases}\left|x-2015\right|^{2015}>1\\\left|x-2016\right|^{2016}>0\end{cases}}\)
\(\Leftrightarrow\left|x-2015\right|^{2015}+\left|x-2016\right|^{2016}>1+0=1\) (vô nghiệm)
Vậy phương trình có 2 nghiệm là \(\left(2015;2016\right)\)
LM
27 tháng 4 2017
*)Xét x < 2015
=> |x - 2016| > 1 <=> |x - 2016|2016 > 1
=> x < 2015 không là nghiệm của pt
**)Xét x > 2016
=> |x - 2015| > 1 <=> |x - 2015|2015 > 1
=> x > 2016 không là nghiệm của pt
***) Xét 2015 < x < 2016
=> 0 < |x - 2015| < 1 (1)
0 < |x - 2016| = |2016 - x|< 1 (2)
=> |x - 2015| + |x - 2016| = |x - 2015| + |2016 - x| = x - 2015 + 2016 - x = 1
Mà: |x - 2015| > |x - 2015|2015 (theo (1)) và |x - 2016| > |x - 2016|2016 (theo (2))
=> |x - 2015|2015 + |x - 2016|2016 < |x - 2015| + |x - 2016| = 1
Vậy phương trình chỉ có 2 nghiệm là x1 = 2015 và x2 = 2016
5 tháng 12 2023
Bài 4:
a: Thay x=-1 và y=0,5 vào y=ax+1, ta được:
\(a\cdot\left(-1\right)+1=0,5\)
=>\(a\cdot\left(-1\right)=0,5-1=-0,5\)
=>a=0,5
b: Khi a=0,5 thì \(y=0,5\cdot x+1\)
Lập bảng giá trị:
| x | -1 | 0 | 1 |
| y=0,5x+1 | 0,5 | 1 | 1,5 |
Vẽ đồ thị:
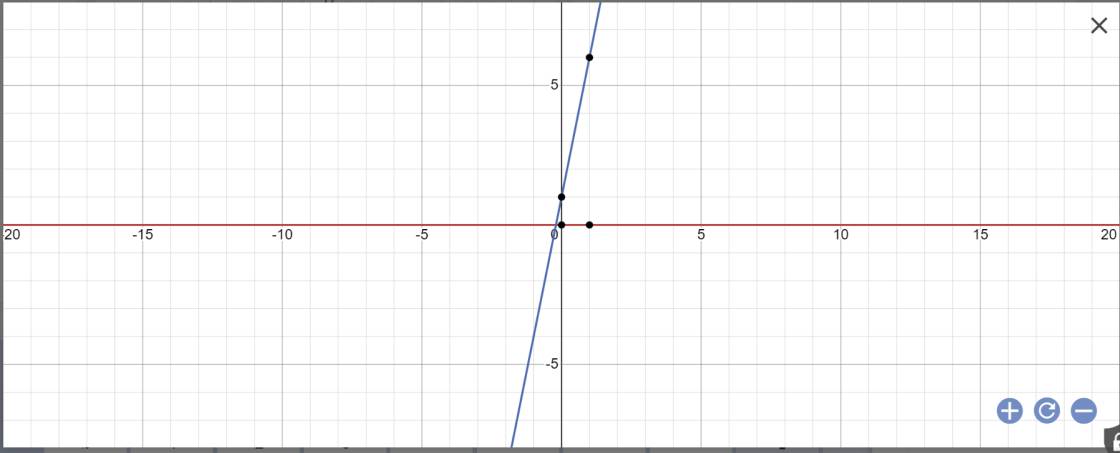
Bài 3:
a:
b: Tọa độ A là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=-0+4=4\end{matrix}\right.\)
Vậy: A(0;4)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0-4=-4\end{matrix}\right.\)
vậy: B(0;-4)
Tọa độ C là:
\(\left\{{}\begin{matrix}-x+4=x-4\\y=x-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-8\\y=x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=4-4=0\end{matrix}\right.\)
Vậy: C(4;0)
c: A(0;4); B(0;-4); C(4;0)
\(AB=\sqrt{\left(0-0\right)^2+\left(-4-4\right)^2}=\sqrt{0^2+\left(-8\right)^2}=8\)
\(AC=\sqrt{\left(4-0\right)^2+\left(0-4\right)^2}=\sqrt{4^2+4^2}=4\sqrt{2}\)
\(BC=\sqrt{\left(4-0\right)^2+\left(0+4\right)^2}=\sqrt{4^2+4^2}=4\sqrt{2}\)
Vì \(CA^2+CB^2=AB^2\)
nên ΔABC vuông tại C
=>\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot4\sqrt{2}\cdot4\sqrt{2}=2\sqrt{2}\cdot4\sqrt{2}=16\)
5 tháng 12 2023
Bài 2:
a: Thay x=2 và y=0 vào y=(m-2)x+m-1, ta được:
\(2\left(m-2\right)+m-1=0\)
=>\(2m-4+m-1=0\)
=>3m-5=0
=>3m=5
=>\(m=\dfrac{5}{3}\)
b: Thay x=0 và y=2 vào y=(m-2)x+m-1, ta được:
\(0\cdot\left(m-2\right)+m-1=2\)
=>m-1=2
=>m=3
Bài 1:
a:
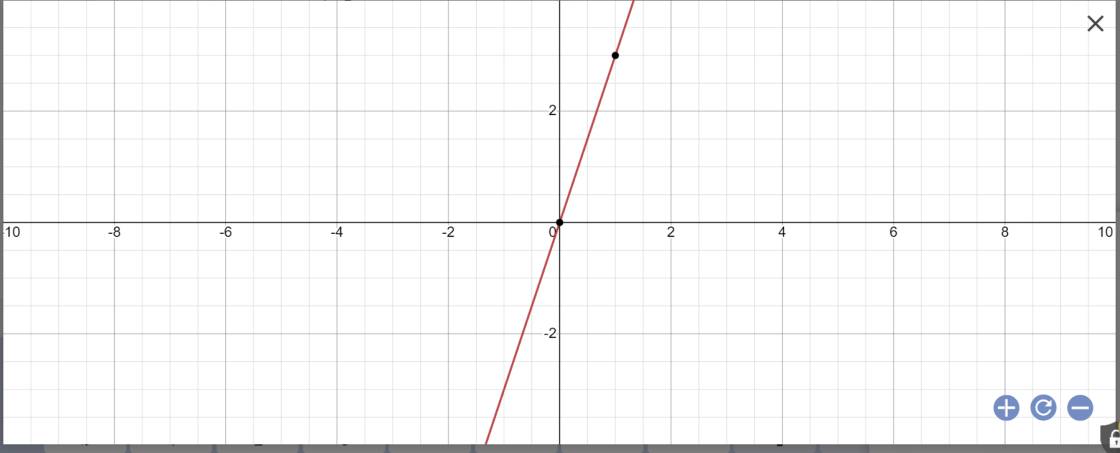
b: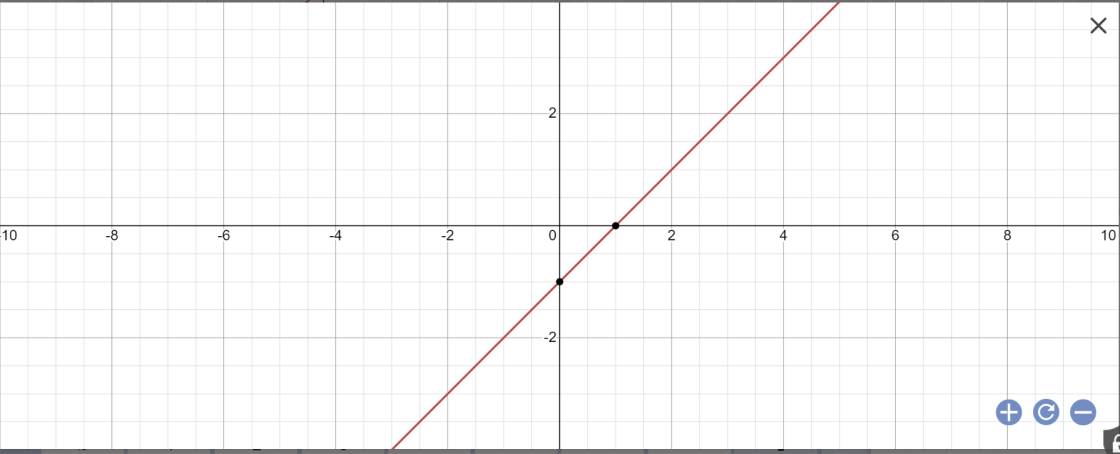 
c:
NL
4 tháng 4 2018
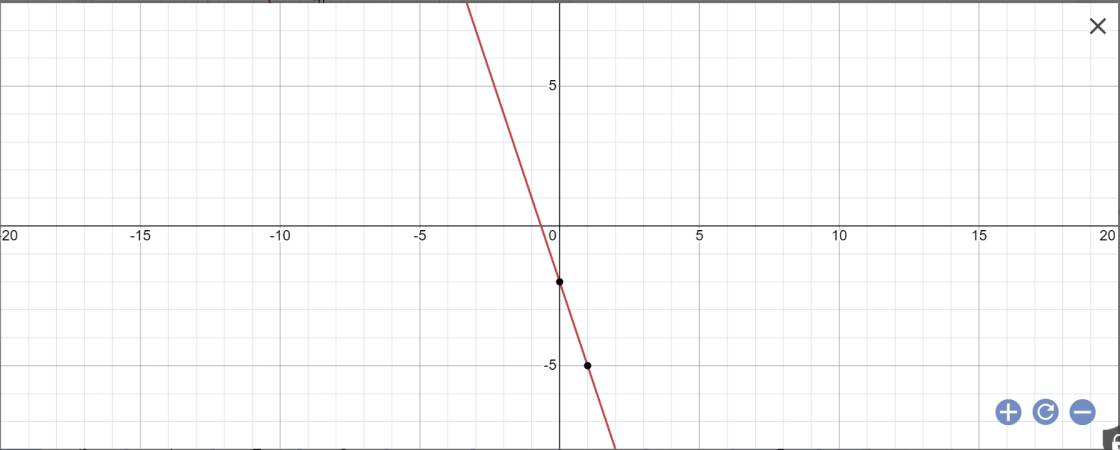
mình tìm không tháy bạn ơi ~ chủ yếu là mình nhờ mấy bạn từng học qua rồi chỉ giúp những dạng chủ yếu,mẹo vặt các loại đấy bạn !! không phải mình tìm đề đâu ~~`
LK
9
26 tháng 4 2017
https://www.facebook.com/boy.capricorn.official
mình là hsg toán 8, kb vs face mình đi
-->(x+2)(x+5)(x+3)(x+4)=24-->(x^2+7x+10)(x^2+7x+12)=24
đặt a=x^2+7x+11
-->a^2-1=24-->.....
Câu 1: Đơn thức là: \(3xy^2z^3\)
⇒ Chọn D
Câu 2: Hai đơn thức đồng dạng là: \(\dfrac{1}{2}x^2y^2\) và \(-3x^2y^2\)
⇒ Chọn C
Câu 3: Hằng đẳng thức là: \(3\left(x+y\right)=3x+3y\)
⇒ Chọn B
Câu 4: \(x^2-...=\left(x-4\right)\left(x+4\right)\Rightarrow x^2-...=x^2-4^2\text{⇒}...=4^2=16\)
⇒ Chọn A