
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 5:
\(\dfrac{x}{y}=a\Rightarrow\dfrac{x}{a}=\dfrac{y}{1}=\dfrac{x-y}{a-1}=\dfrac{x+y}{a+1}\)
\(\Rightarrow\dfrac{x+y}{x-y}=\dfrac{a+1}{a-1}\)
Câu 6:
\(9x=5y\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{9}=\dfrac{3x}{15}=\dfrac{2y}{18}=\dfrac{3x-2y}{15-18}=\dfrac{12}{-3}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).5=-20\\y=\left(-4\right).9=-36\end{matrix}\right.\)
Câu 7:
\(\dfrac{x}{-5}=\dfrac{y}{7}=\dfrac{x+y}{-5+7}=\dfrac{-10}{2}=-5\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-5\right).\left(-5\right)=25\\y=\left(-5\right).7=-35\end{matrix}\right.\)

ta có 5x=3y và 2x-y=3
5x=3y=>\(\frac{x}{3}=\frac{y}{5}\)
\(\frac{x}{3}=\frac{2x}{3.2}=\frac{2x}{6}\)=>\(\frac{2x}{6}=\frac{y}{5}\)
áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{2x}{6}=\frac{y}{5}=\frac{2x-y}{6-5}=\frac{3}{1}=3\)
*\(\frac{x}{3}=3=>x=3.3=9\)
*\(\frac{y}{5}=3=>y=3.5=15\)
vậy x=9và y=15

Chép đề lên nhé làm cho bạn đã là miễn phí rồi bạn còn bắt người ta dở sách à :)

3A = 3 - 3^2 + 3^3 - 3^4 + ... -3^2004 + 3^2005
3A + A = 3 - 3^2 + 3^3 -3^4 + ... -3^2004 + 3^2005 +1 - 3 + 3^2- 3^3 + 3^4 - ....-3^2003+3^2004
4A = 3^2005 + 1
=> 4A - 1 = 3^2005 là lũy thừa của 3 => ĐPCM
Mình có nghe nói là 2 nhà toán học Alfred North Whitehead và Bertrand Russell đã chứng minh 1+1=2 trong quyển Principa Mathemaa (tạm dịch: nền tảng của toán học). Họ đã mất hơn 360 trang để chứng minh điều này. Thầy giáo bạn gãi đầu là phải.
Phép chứng minh này dựa trên một bộ 9 tiên đề về tập hợp gọi tắt là ZFC (Zermelo–Fraenkel). Rất nhiều lý thuyết số học hiện đại dựa trên những tiên đề này. Nếu có người chứng minh được một trong những tiên đề đó là sai (VD: 2 tập hợp có cùng các phần tử mà vẫn không bằng nhau) thì rất có thể dẫn đến 1+1 != 2

Bài 4: AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 5:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{2}=\dfrac{\widehat{B}}{3}=\dfrac{\widehat{C}}{4}=\dfrac{180^0}{9}=20^0\)
Do đó: \(\widehat{A}=40^0;\widehat{B}=60^0;\widehat{C}=80^0\)
=>BC<AC<AB

Bài 1:
a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI

\(\left\{{}\begin{matrix}x=\dfrac{5}{9}y\\x=\dfrac{10}{21}z\\2x=3y+z=50\end{matrix}\right.\)\(\Rightarrow2x-\dfrac{27}{5}+\dfrac{21}{10}x=50\)
\(\left\{{}\begin{matrix}x=\dfrac{500}{15}\\y=-\dfrac{900}{13}\\-\dfrac{1050}{13}\end{matrix}\right.\)
b: Ta có: \(\dfrac{x}{-3}=\dfrac{y}{7}\)
nên \(\dfrac{x}{6}=\dfrac{y}{-14}\left(1\right)\)
Ta có: \(\dfrac{y}{-2}=\dfrac{z}{5}\)
nên \(\dfrac{y}{-14}=\dfrac{z}{35}\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra \(\dfrac{x}{6}=\dfrac{y}{-14}=\dfrac{z}{35}\)
hay \(\dfrac{-2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{-2x}{12}=\dfrac{4y}{-56}=\dfrac{5z}{175}=\dfrac{-2x-4y+5z}{12+56+175}=\dfrac{146}{243}\)
Do đó: \(\left\{{}\begin{matrix}x=\dfrac{292}{81}\\y=-\dfrac{2044}{243}\\z=\dfrac{5110}{243}\end{matrix}\right.\)
 giải dùm mình với mình sắp phải nộp rồi
giải dùm mình với mình sắp phải nộp rồi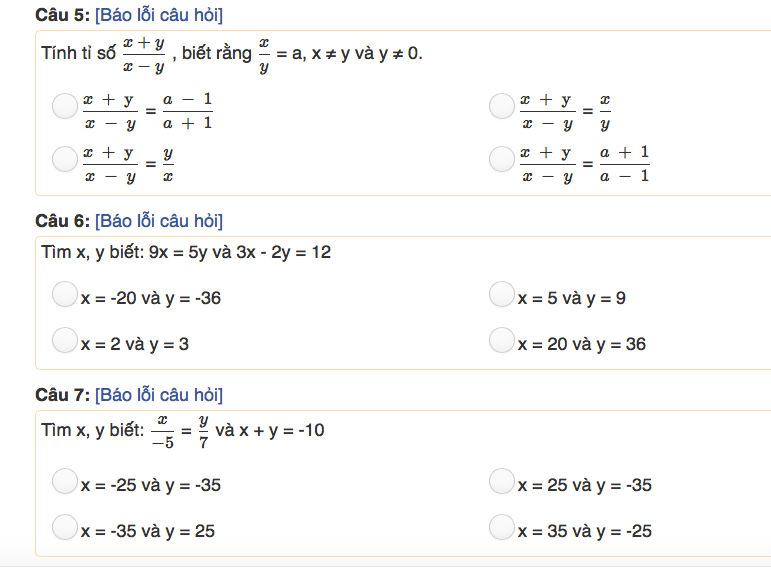



Bài 1:
\(\frac{3}{5}.x=\frac{2}{3}.y\Rightarrow\frac{3x}{5}=\frac{2y}{3}\Rightarrow\frac{x}{15}=\frac{y}{9}=k\)
=> \(\begin{cases}x=15k\\y=9k\end{cases}\)
ta có:
(15k)2.(9k)2=38
225k2.81k2=38
18225k4=38
k4=\(\sqrt[4]{18225}\)
x=\(15\sqrt[4]{18225}\)
y=\(9.\sqrt[4]{18225}\)
Bài 2:
\(\frac{x+16}{9}=\frac{y-25}{16}=\frac{z+9}{25}=\frac{x+16+y-25}{9+16}=\frac{x+y-9}{25}\)
=> \(\left[\begin{array}{nghiempt}TH1:z+9=x+y-9=0\\TH2:z+9=x+y-9\ne0\end{array}\right.\)
TH1:
z+9=x+y-9=0
=> z=-9 và x+y=0=> x=-y hoặc x=y=0
+với x=y=0
2x3-1=15(1)
thay x vào (1) ta có:
2.03-1=-1 \(\ne15\)(loại)
+ với z=-9 và x=-y ta có:
2.x3-1=15
=>2.x3=16
=> x3=8
=> x3=23
=> x=2 => x=-2
=>x+y+z=-9+2-2=-9
Th2:
với z+9=x+y-9\(\ne0\)
=> z=x+y-18
x=z-y+18
thay x vào (1) ta có:
2.(z-y+18)3-1=15
2(z2-2yz+y2+54z2-108yz+54y2+972z-972y +5832)= 16
2z2-4yz+2y2+108z2-216yz+105y2+1944z -1944y +11664=16
..........................................................................................
vậy x+y+z=-9 trong TH z=-9, x=2 và y=-1
Ở bài 1 chắc mk làm sai vì lớp 7 đã học căn bậc 4 đâu. :)