TT
4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
MT
3
MT
4
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
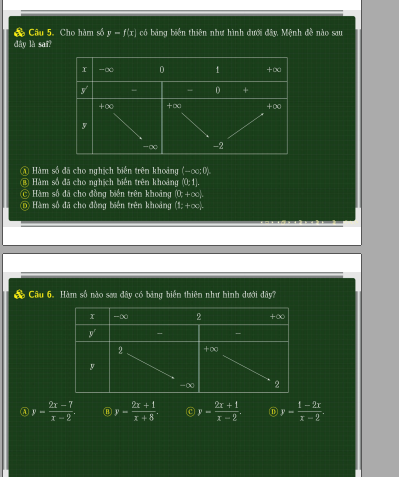
Câu 5:
Nhìn BBT trên \(\left(0;+\infty\right)\) ta thấy trên \(\left(0;1\right)\) đồ thị là đường đi xuống (nghịch biến) nên hàm đồng biến trên toàn miền \(\left(0;+\infty\right)\) là sai
Câu 6:
Từ BBT ta thấy hàm nghịch biến trên các khoảng xác định
\(\Rightarrow\) Loại 2 phương án A và B (ở 2 phương án này hàm đồng biến do y' lần lượt là \(\dfrac{3}{\left(x-2\right)^2}>0\) và \(\dfrac{15}{\left(x+8\right)^2}>0\))
Còn lại 2 phương án C và D, nhìn BBT ta thấy \(y=2\) là tiệm cận ngang (giá trị của y tại x vô cực)
\(\lim\limits_{x\rightarrow\infty}\dfrac{2x+1}{x-2}=2\) (đúng) nên chọn C
7.
Từ BBT ta thấy đây là BBT của hàm bậc 3 \(\Rightarrow\) loại B và D
Từ BBT, y'=0 có 2 nghiệm \(x=0,x=2\)
Ở đáp án A, \(y'=x^2+2x=0\Rightarrow x=0;x=-2\) (ktm)
Nên C đúng (\(y'=x^2-2x=0\Rightarrow x=0;2\))
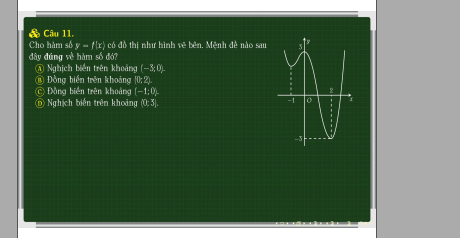
11.
Nhìn đồ thị, ta thấy trên \(\left(-1;0\right)\) đồ thị chỉ có hướng đi lên \(\Rightarrow\) đồng biến trên (-1;0) nên C đúng
(A sai vì trên (-3;0) đồ thị có khoảng đi lên (đồng biến) ở (-1;0)
B sai vì trên (0;2) đồ thị đi xuống => nghịch biến chứ ko phải đồng biến
D sai vì trên (2;3) đồ thị đi lên (đồng biến)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
5C, 6C, 7C, 11C
Cả 4 câu đều C luôn, kì quái thật
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 8 2021
9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
1.
\(y'=x^2-6x+5=0\Rightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
Dấu của y' trên trục số:
Hàm đồng biến trên các khoảng \(\left(-\infty;1\right)\) và \(\left(5;+\infty\right)\)
Hàm nghịch biến trên \(\left(1;5\right)\)
3.
TXĐ: \(D=R\backslash\left\{2\right\}\)
\(y'=\dfrac{-5}{\left(x-2\right)^2}< 0;\forall x\in D\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 9 2021
4.
\(y'=4x^3+4x=4x\left(x^2+1\right)=0\Rightarrow x=0\)
Dấu của y':
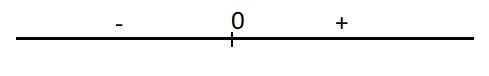
Hàm đồng biến trên \(\left(0;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\)
6.
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-1;1\right)\)
HT
9 tháng 3 2021
Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{0}\Leftrightarrow\overrightarrow{A'G}+\overrightarrow{GA}+\overrightarrow{B'G}+\overrightarrow{GB}+\overrightarrow{C'G}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Goi G la trong tam tam giac A'B'C'
Lai co: \(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{0}\)
\(\Rightarrow G'\equiv G\Rightarrow G'=\left(1;0;-2\right)\)
AN
2
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 8 2021
\(y'=-3mx^2+2x-3\)
Hàm nghịch biến trên khoảng đã cho khi với mọi \(x\in\left(-3;0\right)\) ta có:
\(-3mx^2+2x-3\le0\)
\(\Leftrightarrow2x-3\le3mx^2\)
\(\Leftrightarrow\dfrac{2x-3}{3x^2}\le m\)
\(\Rightarrow m\ge\max\limits_{\left(-3;0\right)}\left(\dfrac{2x-3}{3x^2}\right)\)
Xét hàm \(f\left(x\right)=\dfrac{2x-3}{3x^2}\Rightarrow f'\left(x\right)=\dfrac{2\left(3-x\right)}{3x^3}< 0;\forall x\in\left(-3;0\right)\)
\(\Rightarrow f\left(x\right)>f\left(-3\right)=-\dfrac{1}{3}\)
\(\Rightarrow m\ge-\dfrac{1}{3}\)
14.
\(y'=2x^3-4x=2x\left(x^2-2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-\sqrt{2}\\x=\sqrt{2}\end{matrix}\right.\)
\(y''=6x-4\)
\(\Rightarrow y''\left(0\right)=-4< 0\Rightarrow x=0\) là điểm cực đại
\(y\left(0\right)=-3\)
\(\Rightarrow\) Điểm cực đại của đồ thị hàm số là \(\left(0;-3\right)\)
12.
\(y'=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
\(y''=6x\)
\(\Rightarrow\left\{{}\begin{matrix}y''\left(1\right)=6>0\\y''\left(-1\right)=-6< 0\end{matrix}\right.\) \(\Rightarrow x=-1\) là điểm cực đại
\(\Rightarrow\)Giá trị cực đại của hàm số là \(y\left(-1\right)=3\)