K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VH
0
13 tháng 3 2017
Ta có:\(\left(-5a^2b^4c^6\right)^7-\left(9a^3bc^5\right)^8=0\)
\(\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}=0\)
Vì \(a^{14}b^{28}c^{42}\ge0\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}\le0\)
\(a^{24}b^8c^{40}\ge0\Rightarrow9^8a^{24}b^8c^{40}\ge0\)
\(\Rightarrow\left(-5\right)^7a^{14}b^{28}c^{42}-9^8a^{24}b^8c^{40}\le0\)
Mà VP=0
Dấu "=" xảy ra khi
\(\left(-5\right)^7a^{14}b^{28}c^{42}=0\) và \(9^8a^{24}b^8c^{40}=0\)
\(\Rightarrow a=b=c=0\)
\(\Rightarrow A=a+b+c=0+0+0=0\)
2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)
Cậu nào giải được giải giúp tớ với 
Tớ camon người giúp tớ nhiều lắm ạ 
Help me
TT
7 tháng 10 2017
\(\left(x-3\right).\left(x-2015\right)< 0\)
\(\Rightarrow\left(x-3\right)và\left(x-2015\right)\) phải khác dấu
\(\Rightarrow\left(x-3\right)< \left(x-2015\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3>0\\x-2015< 0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x>3\\x< 2015\end{matrix}\right.\)
\(\Rightarrow3< x< 2015\)
\(\Rightarrow x\in\left\{4;5;6;7;8;...;2013;2014\right\}\)
( ko bt đúng hay sai nx )
7 tháng 10 2017
thám tử
\(\left(x-3\right)\left(x-2015\right)< 0\)
Với mọi \(x\in R\) thì:
\(x-2015< x-3\)
Khi đó: \(\left\{{}\begin{matrix}x-2015< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 2015\\x>3\end{matrix}\right.\)
Nên \(3< x< 2015\)
19 tháng 3 2017
Ta có:\(2009^{20}=\left(2009^2\right)^{10}=4036081^{10}< 20092009^{10}\)
Vậy \(2009^{20}< 20092009^{10}\)
help me
H
25 tháng 7 2017
Theo mình nghĩ thì đề thiếu là tam giác ABC vuông tại A nhé!
Bạn xem lại đề!:)
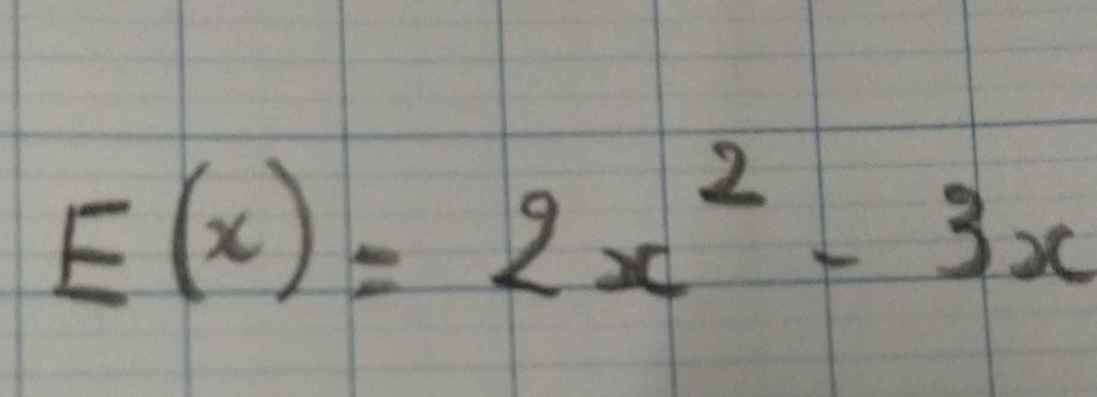
Đặt E(x)=0
\(\Leftrightarrow2x^2-3x=0\)
\(\Leftrightarrow x\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{3}{2}\right\}\)
Đặt E(x)=0
⇔2x2−3x=0⇔2x2−3x=0
⇔x(2x−3)=0⇔x(2x−3)=0
⇔[x=02x−3=0⇔[x=02x=3⇔⎡⎣x=0x=32⇔[x=02x−3=0⇔[x=02x=3⇔[x=0x=32
Vậy: S={0;32}