K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H
12 tháng 6 2021
Bạn nên tự làm bài trước bài nào khó thì lên đây hỏi và bảo mn giải thích bạn sẽ hiểu hơn và mn cũng sẽ đỡ tốn nhiều thời gian hơn
SD
2
26 tháng 2 2023
câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)
20 tháng 6 2023
3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 4 2022
Giả sử \(x_1< x_2\)
Gọi A, B là 2 điểm biểu diễn \(x_1;x_2\) trên \(Ox\Rightarrow A\left(x_1;0\right)\) ; \(B\left(x_2;0\right)\)
\(OA=\left|x_1\right|;OB=\left|x_2\right|\)
\(\Rightarrow AB=\left|x_2-x_1\right|\)
Trong tam giác vuông OAN: \(OA^2+ON^2=AN^2\Rightarrow AN^2=x_1^2+b^2\)
Trong tam giác vuông OBN: \(OB^2+ON^2=BN^2\Rightarrow BN^2=x_2^2+b^2\)
Do tam giác ABN vuông tại N:
\(\Rightarrow AN^2+BN^2=AB^2\)
\(\Rightarrow x_1^2+x_2^2+2b^2=\left(x_2-x_1\right)^2\)
\(\Rightarrow2b^2=-2x_1x_2\Rightarrow b^2=-x_1x_2\)
\(\Rightarrow b^2=1011\Rightarrow b=\sqrt{1011}\)
LT
1
20 tháng 10 2023
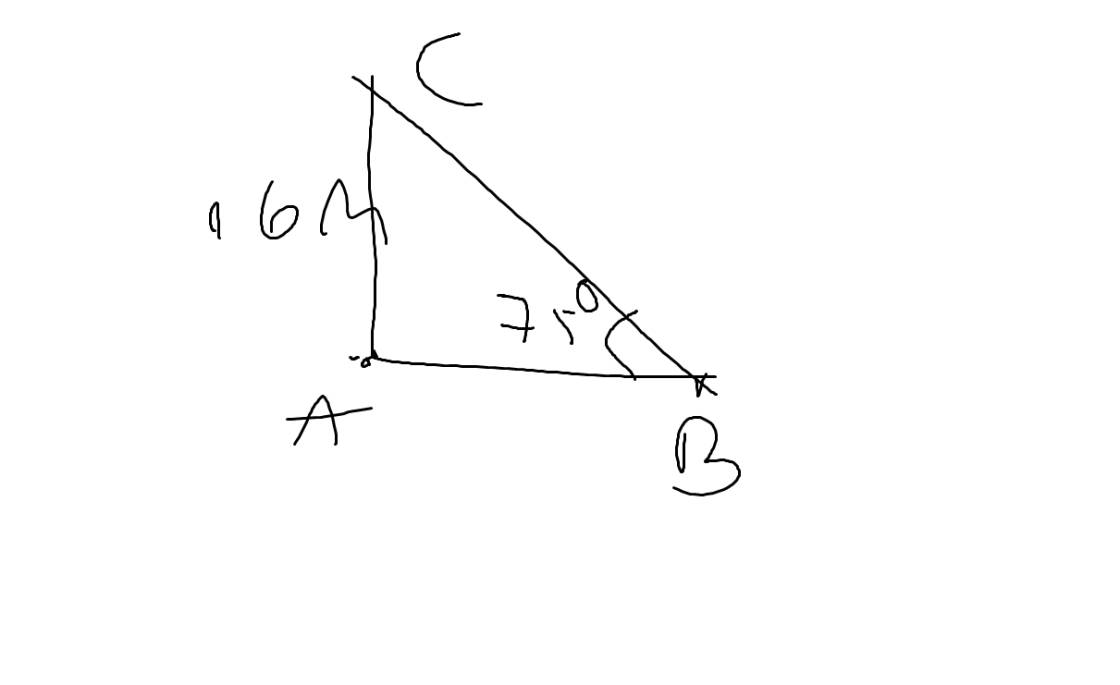
Gọi A,B lần lượt là hai mốc của bờ sông. Gọi điểm C là điểm nằm trên đường thước dây vuông góc với bờ sông tại A
=>AB vuông góc AC tại A
Theo đề, ta có: AC=16m \(\widehat{ABC}=75^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AB=\dfrac{AC}{tanB}=16:tan75\simeq4,3\left(m\right)\)
Q9
1
14 tháng 12 2021
\(\Leftrightarrow2\sqrt{x-4}=5\left(x\ge4\right)\\ \Leftrightarrow\sqrt{x-4}=\dfrac{5}{2}\\ \Leftrightarrow x-4=\dfrac{25}{4}\\ \Leftrightarrow x=\dfrac{41}{4}\left(tm\right)\)
11 tháng 8 2021
a, \(\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}-3}\)
\(=\dfrac{\sqrt{3}-3}{9-5\sqrt{3}}-\dfrac{\sqrt{3}-2}{9-5\sqrt{3}}\)
\(=\dfrac{-1}{9-5\sqrt{3}}\)
b, \(\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right)\cdot\left(\sqrt{x}-\dfrac{4}{\sqrt{x}}\right)\) (ĐK: x > 0; \(x\ne1\) )
\(=\left(\dfrac{x-3\sqrt{x}+2}{x-4}-\dfrac{x+4\sqrt{x}+4}{x-4}\right)\cdot\left(\dfrac{x}{\sqrt{x}}-\dfrac{4}{\sqrt{x}}\right)\)
\(=\left(\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-4}{x-4}\right)\cdot\left(\dfrac{x-4}{\sqrt{x}}\right)\)
\(=\dfrac{-7\sqrt{x}-2}{x-4}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{-7\sqrt{x}-2}{\sqrt{x}}\)
c, \(\dfrac{1}{\sqrt{x}-1}-\dfrac{3}{x\sqrt{x}-1}+\dfrac{1}{x+\sqrt{x}+1}\) (ĐK: \(x\ge0;x\ne1\) )
\(=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}\right)^3-1^3}-\dfrac{3}{\left(\sqrt{x}\right)^3-1^3}+\dfrac{\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{x+\sqrt{x}+1-3+\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{2\sqrt{x}+x-3}{\left(\sqrt{x}\right)^3-1^3}\)
P/s: vì chữ bạn hơi xấu, mình dịch chưa chắc đúng nên có gì sai bạn thông cảm nhé. ^^
a: Để biểu thức có nghĩa thì 3x-5>=0
hay x>=5/3
b: \(=20\sqrt{3}-3\cdot6\sqrt{3}+\dfrac{1}{2}\cdot10\sqrt{3}=2\sqrt{3}+5\sqrt{3}=7\sqrt{3}\)
Cảm ơn nhiều ạ