K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AM
0
VT
0
31 tháng 7 2021
câu 1 là 2 cạnh góc vuông hay 1 cạnh góc vuông và cạnh huyền thế
câu 2 AC là cạnh góc vuông hay cạnh huyền
31 tháng 7 2021
1. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\cos B=\dfrac{AB}{BC}=\dfrac{6}{10}\Rightarrow B=53^O\\ C=A-B=90^o-53^o=37^o\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-6^2}=8\)
2. Xét \(\Delta\)ABC vuông tại A, theo tỉ số lượng giác ta có
\(\sin C=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{\sin C}=\dfrac{5}{sin30}=10\\ AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-5^2}=5\sqrt{3}\\ B=A-C=90^o-30^o=60^o\)
VT
0
7 tháng 8 2021
a, Thay x = 49 vào biểu thức Q ta được : \(\dfrac{7+1}{7+2}=\dfrac{8}{9}\)
b, Với x >= 0 ; \(x\ne1\)
\(P=\left(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}+1-2\sqrt{x}}{x-1}\right)=\dfrac{x-2\sqrt{x}+1}{x-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
\(S=P.Q\Rightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+1}.\dfrac{\sqrt{x}+1}{\sqrt{x}+2}=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
c, \(S=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}=\dfrac{\sqrt{x}+2-3}{\sqrt{x}+2}=1-\dfrac{3}{\sqrt{x}+2}\)
\(\sqrt{x}+2\ge2\Rightarrow\dfrac{-3}{\sqrt{x}+2}\ge-\dfrac{3}{2}\)
\(\Rightarrow S\ge1-\dfrac{3}{2}=-\dfrac{1}{2}\)
Dấu ''='' xảy ra khi x = 0
18 tháng 9 2021
\(4,\\ 2.B=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\left(x>0\right)\\ B=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\)
\(3.x=\sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}=\left(3+\sqrt{2}\right)+\left(3-\sqrt{2}\right)=6\)
Thay vào B, ta được \(B=\dfrac{6-3\sqrt{6}+2}{\sqrt{6}}=\dfrac{6\sqrt{6}-18+2\sqrt{6}}{6}=\dfrac{4\sqrt{6}-9}{3}\)
\(4.B=0\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=0\Leftrightarrow x-3\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
\(7.B\in Z\Leftrightarrow\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}-3+\dfrac{2}{\sqrt{x}}\in Z\\ \Leftrightarrow\dfrac{2}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\inƯ\left(2\right)=\left\{-2;-1;1;2\right\}\\ \Leftrightarrow x\in\left\{1;4\right\}\left(\sqrt{x}>0\right)\)
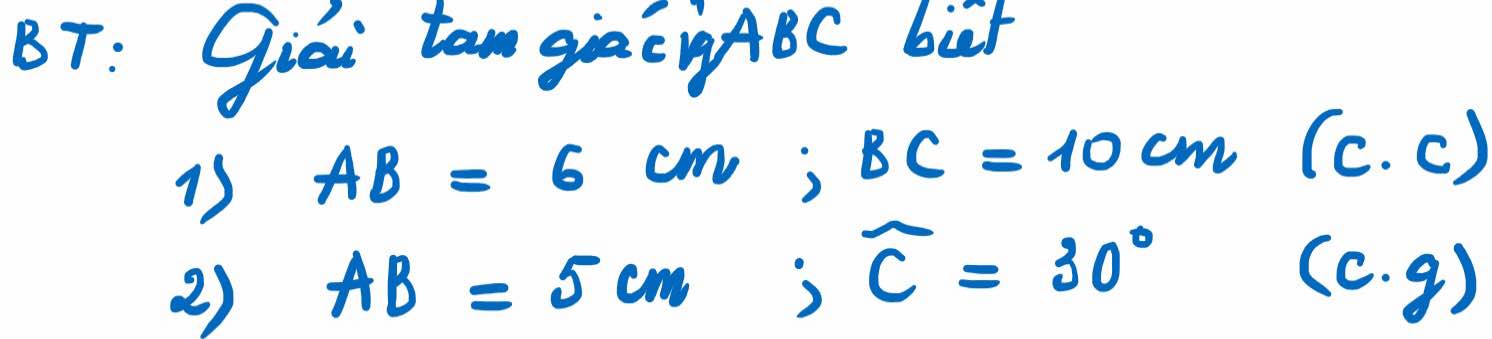
a: Xét ΔCHD vuông tại H có HM là đường cao ứng với cạnh huyền CD
nên \(CM\cdot CD=CH^2\left(1\right)\)
Xét ΔCHE vuông tại H có HN là đường cao ứng với cạnh huyền CE
nên \(CN\cdot CE=CH^2\left(2\right)\)
Từ (1) và (2) suy ra \(CM\cdot CD=CN\cdot CE\)
b: Ta có: \(CM\cdot CD=CN\cdot CE\)
nên \(\dfrac{CM}{CE}=\dfrac{CN}{CD}\)
Xét ΔCMN và ΔCED có
\(\dfrac{CM}{CE}=\dfrac{CN}{CD}\)
\(\widehat{MCN}\) chung
Do đó: ΔCMN\(\sim\)ΔCED