K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 4 2021
Đặt E(x)=0
\(\Leftrightarrow2x^2-3x=0\)
\(\Leftrightarrow x\left(2x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\2x=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy: \(S=\left\{0;\dfrac{3}{2}\right\}\)
5 tháng 4 2021
Đặt E(x)=0
⇔2x2−3x=0⇔2x2−3x=0
⇔x(2x−3)=0⇔x(2x−3)=0
⇔[x=02x−3=0⇔[x=02x=3⇔⎡⎣x=0x=32⇔[x=02x−3=0⇔[x=02x=3⇔[x=0x=32
Vậy: S={0;32}
SH
3
A
23 tháng 10 2016
\(0,0\left(3\right)+0,0\left(16\right)\)\(=\frac{1}{30}+\frac{16}{990}\)\(=\)\(\frac{33}{990}+\frac{16}{990}=\frac{49}{990}\)
LT
3
K
13 tháng 8 2019
(x + 2)(x + 5) < 0
Th1: x + 2 > 0 => x > -2
x + 5 < 0 => x < -5
=> Vô lý
Th2: x + 2 < 0 => x < -2
x + 5 > 0 => x > -5
=> -5 < x < -2
13 tháng 8 2019
Ta có : (x+2)(x+5)<0
=> x+2 và x+5 là hai số nguyên trái dấu
mà x+5 > x+2
=> \(\hept{\begin{cases}x+5>0\\x+2< 0\end{cases}}\)
=> \(\hept{\begin{cases}x>-5\\x< 2\end{cases}}\)
=> \(-5< x< 2\)
=> \(x\in\left\{-4;-3;-2;-1;0;1\right\}\)
~ học tốt nha ~
LS
3
30 tháng 8 2015
(-4,9)+5,5+4,9+(-5,5)
=[(-4,9)+4,9]+[5,5+(-5,5)]
=(4,9-4,9)+(5,5-5,5)
=0+0
=0
VD
2
1 tháng 5 2023
`P(x)=2x^3+x^2+5-3x+3x^2-2x^3-4x^2+1`
`= (2x^3-2x^3)+(x^2+3x^2-4x^2)-3x+(5+1)`
`= -3x+6`
Thay `x=0`
`P(0)=-3*0+6=6`
Thay `x=-1`
`P(-1)=(-3)*(-1)+6=3+6=9`
Thay `x=1/3`
`P(1/3)=(-3)*1/3+6=-1+6=5`
VD
2
H
3 tháng 5 2023
\(a,2x^3.\left(-3x^2+5\right)=2x^3.\left(-3x^2\right)+2x^3.5=-6x^{3+2}+10x^3\\ =-6x^5+10x^3\\ b,-2x^4+5x^4=\left(-2+5\right)x^4=3x^4\)
VD
2
H
3 tháng 5 2023
a,
\(C\left(x\right)=A\left(x\right)+B\left(x\right)=x-2x^3+3-4+2x^2+x^3-2x\\ =\left(-2x^3+x^3\right)+\left(2x^2\right)+\left(x-2x\right)+\left(3-4\right)\\ =-x^3+2x^2-x-1\)
b, Thay \(x=2\) vào \(C\left(x\right)\)
\(\Rightarrow-\left(2\right)^3+2.2^2-2-1=-3\ne0\)
\(\Rightarrow x=2\) không là nghiệm của đa thức
VD
2
11 tháng 5 2023
\(A=x^5-4x^4+x^3+x^4-4x^3+x^2+5x^2-20x+5+2023\)
=2023
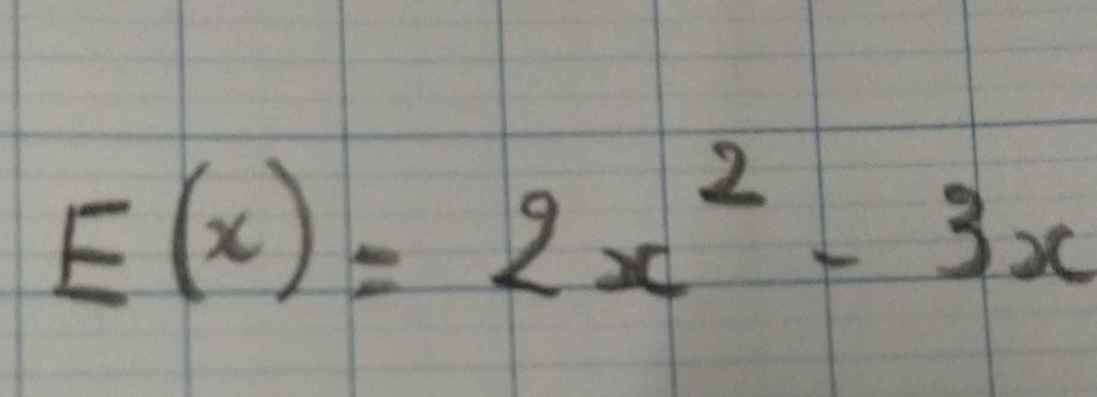
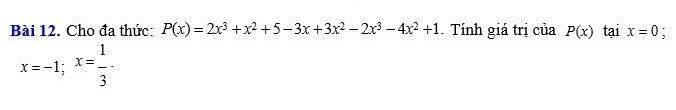
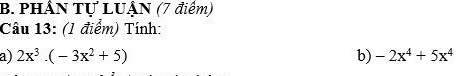
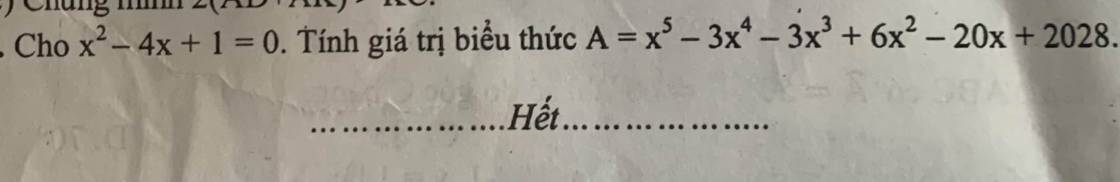
d. \(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
\(\Rightarrow\left(x-2\right)\left(x+7\right)=\left(x-1\right)\left(x+4\right)\)
\(\Rightarrow x^2+5x-14=x^2+3x-4\)
\(\Rightarrow x^2+5x-x^2-3x=-4+14\)
\(\Rightarrow2x=10\) \(\Rightarrow x=\dfrac{10}{3}\) \(\Rightarrow x=5\)
\(\dfrac{x-2}{x-1}=\dfrac{x+4}{x+7}\)
⇔ \(\dfrac{\left(x-2\right)\left(x+7\right)}{\left(x-1\right)\left(x+7\right)}=\dfrac{\left(x+4\right)\left(x-1\right)}{\left(x+7\right)\left(x-1\right)}\)
⇔ (x - 2)(x + 7) = (x + 4)(x - 1)
⇔ x2 + 7x - 2x - 14 = x2 - x + 4x - 4
⇔ x2 - x2 + 7x - 2x + x - 4x = 14 - 4
⇔ 2x = 10
⇔ x = 10/2 = 5