
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


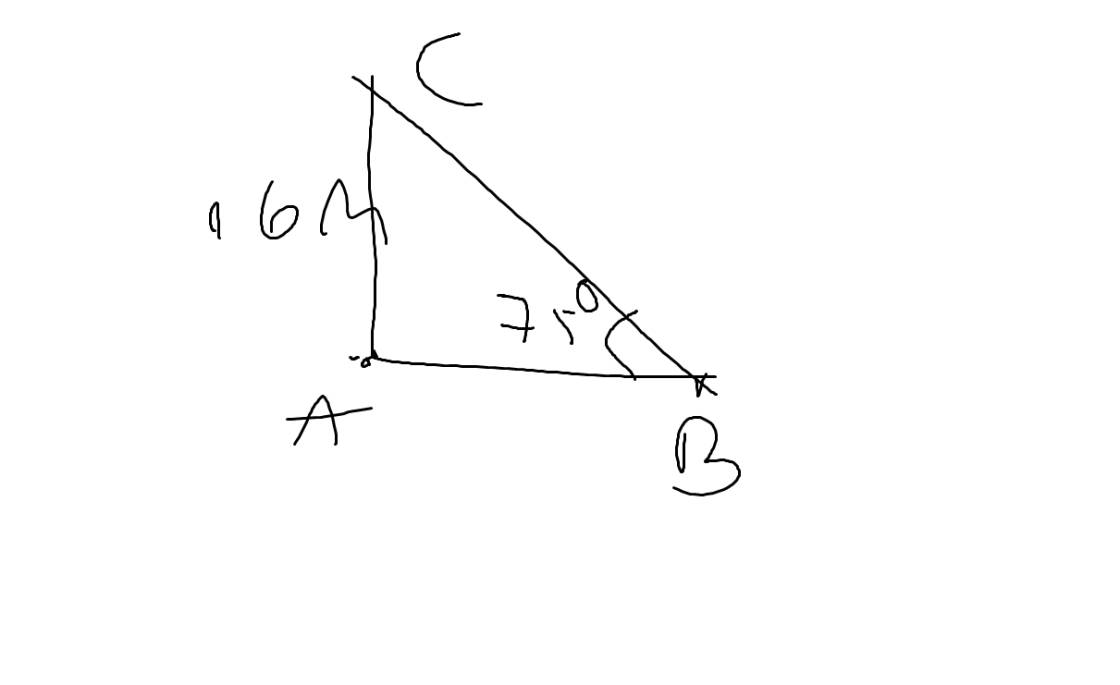
Gọi A,B lần lượt là hai mốc của bờ sông. Gọi điểm C là điểm nằm trên đường thước dây vuông góc với bờ sông tại A
=>AB vuông góc AC tại A
Theo đề, ta có: AC=16m \(\widehat{ABC}=75^0\)
Xét ΔABC vuông tại A có \(tanB=\dfrac{AC}{AB}\)
=>\(AB=\dfrac{AC}{tanB}=16:tan75\simeq4,3\left(m\right)\)



a, \(\dfrac{1}{\sqrt{3}-2}-\dfrac{1}{\sqrt{3}-3}\)
\(=\dfrac{\sqrt{3}-3}{9-5\sqrt{3}}-\dfrac{\sqrt{3}-2}{9-5\sqrt{3}}\)
\(=\dfrac{-1}{9-5\sqrt{3}}\)
b, \(\left(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\right)\cdot\left(\sqrt{x}-\dfrac{4}{\sqrt{x}}\right)\) (ĐK: x > 0; \(x\ne1\) )
\(=\left(\dfrac{x-3\sqrt{x}+2}{x-4}-\dfrac{x+4\sqrt{x}+4}{x-4}\right)\cdot\left(\dfrac{x}{\sqrt{x}}-\dfrac{4}{\sqrt{x}}\right)\)
\(=\left(\dfrac{x-3\sqrt{x}+2-x-4\sqrt{x}-4}{x-4}\right)\cdot\left(\dfrac{x-4}{\sqrt{x}}\right)\)
\(=\dfrac{-7\sqrt{x}-2}{x-4}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{-7\sqrt{x}-2}{\sqrt{x}}\)
c, \(\dfrac{1}{\sqrt{x}-1}-\dfrac{3}{x\sqrt{x}-1}+\dfrac{1}{x+\sqrt{x}+1}\) (ĐK: \(x\ge0;x\ne1\) )
\(=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}\right)^3-1^3}-\dfrac{3}{\left(\sqrt{x}\right)^3-1^3}+\dfrac{\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{x+\sqrt{x}+1-3+\sqrt{x}-1}{\left(\sqrt{x}\right)^3-1^3}\)
\(=\dfrac{2\sqrt{x}+x-3}{\left(\sqrt{x}\right)^3-1^3}\)
P/s: vì chữ bạn hơi xấu, mình dịch chưa chắc đúng nên có gì sai bạn thông cảm nhé. ^^


3.7:
a: =>9x=225
=>x=25
b: =>4x^2=64
=>x^2=16
=>x=4 hoặc x=-4
c; =>4(x+1)=8
=>x+1=2
=>x=1
d: =>9(2-3x)^2=36
=>(3x-2)^2=4
=>3x-2=4 hoặc 3x-2=-4
=>x=2 hoặc x=-2/3
e: =>\(\sqrt{x-2}\left(\sqrt{x+2}-2\right)=0\)
=>x-2=0 hoặc x+2=4
=>x=2

Gọi vận tốc thực là x
Theo đề, ta có: \(\dfrac{54}{x+3}+\dfrac{54}{x-3}=7.5\)
=>\(\dfrac{54x-162+54x+162}{x^2-9}=7.5\)
=>7,5(x^2-9)=108x
=>7,5x^2-108x-67,5=0
=>x=15

\(b,B=\dfrac{x-4+2\sqrt{x}+6-3\sqrt{x}-4}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\\ B=\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\\ c,M=B:A=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{x-\sqrt{x}+2}=\dfrac{\sqrt{x}+1}{x-\sqrt{x}+2}\\ M=\dfrac{x-\sqrt{x}+2-x+2\sqrt{x}-1}{x-\sqrt{x}+2}\\ M=1-\dfrac{x-2\sqrt{x}+1}{x-\sqrt{x}+2}=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\)
Ta có \(\left(\sqrt{x}-1\right)^2\ge0;x-\sqrt{x}+2=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{7}{4}>0\)
Do đó \(\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\ge0\)
\(\Leftrightarrow M=1-\dfrac{\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+2}\le1-0=1\)
Vậy \(M_{max}=1\Leftrightarrow\sqrt{x}=1\Leftrightarrow x=1\left(tm\right)\)
a: Thay \(x=3+2\sqrt{2}\) vào A, ta được:
\(A=\dfrac{3+2\sqrt{2}-\sqrt{2}-1+2}{\sqrt{2}+1+3}=\dfrac{4+\sqrt{2}}{4+\sqrt{2}}=1\)

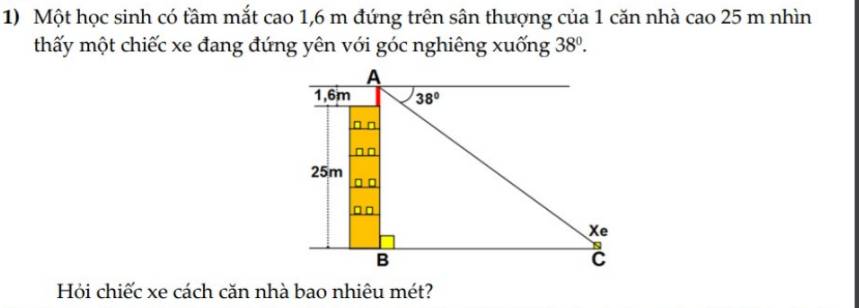




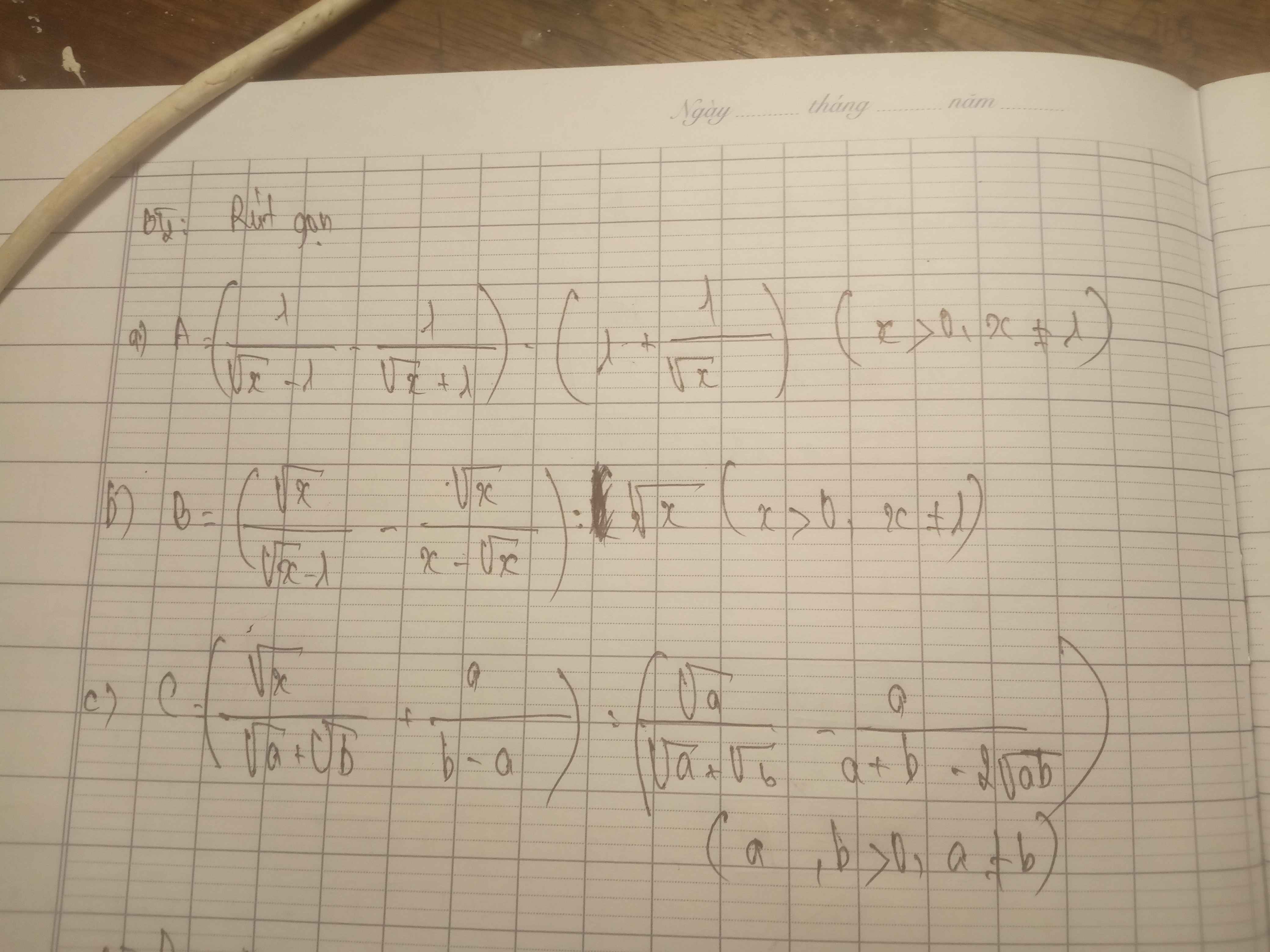
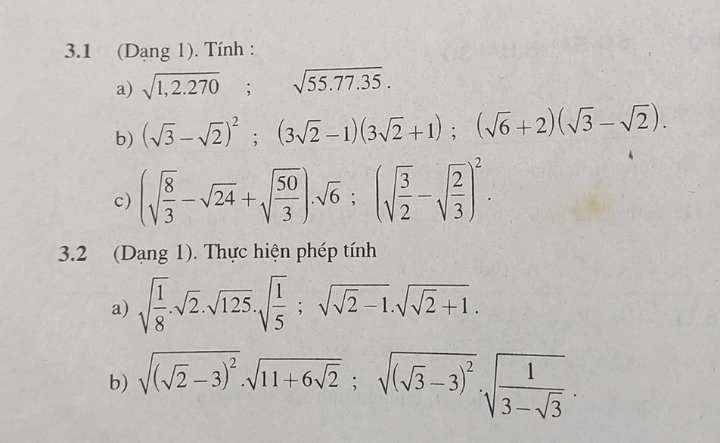
 giúp em giải chi tiết với ạ
giúp em giải chi tiết với ạ


Ta có \(\widehat{ACB}=38^0\) (so le trong)
\(AB=25+1,6=26,6\left(m\right)\)
\(\Rightarrow BC=\dfrac{AB}{tan\widehat{ACB}}=\dfrac{26,6}{tan38^0}\approx34\left(m\right)\)