Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(4x^2-x+1< 0\)
Tam thức f(x) = 4x2 - x + 1 có hệ số a = 4 > 0 biệt thức ∆ = 12 – 4.4 < 0. Do đó f(x) > 0 ∀x ∈ R.
Bất phương trình 4x2 - x + 1 < 0 vô nghiệm.
b) f(x) = - 3x2 + x + 4 = 0
\(\Delta=1^2-4\left(-3\right).4=49\)
\(x_1=\dfrac{-1+\sqrt{49}}{-3}=-1\)
\(x_2=\dfrac{-1-\sqrt{49}}{-3.2}=\dfrac{4}{3}\)
- 3x2 + x + 4 ≥ 0 <=> - 1 ≤ x ≤ .

a. TH1:
\(\left\{{}\begin{matrix}x^2+3x-4< 0\\3-2x>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 1\\x>-4\end{matrix}\right.\\x>\dfrac{3}{2}\end{matrix}\right.\)
TH2:
\(\left\{{}\begin{matrix}x^2+3x-4>0\\3-2x< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x< -4\end{matrix}\right.\\x< \dfrac{3}{2}\end{matrix}\right.\)
Vậy nghiệm của BPT:
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 1\\x>-4\end{matrix}\right.\\x>\dfrac{3}{2}\end{matrix}\right.\) \(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1\\x< -4\end{matrix}\right.\\x< \dfrac{3}{2}\end{matrix}\right.\)

a)
\(\left\{{}\begin{matrix}x^2+x+5< 0\\x^2-6x+1>0\end{matrix}\right.\)
\(\)Ta có
\(x^2+x+5=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{19}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}>0\)
=> Bất phương trình đàu tiên sai, hệ bất phương trình sai
b)
\(\left\{{}\begin{matrix}2x^2+x-6>0\\3x^2-10x+3\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3\right)\left(x+2\right)>0\\\left(x-3\right)\left(3x-1\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x>2\\x< -3\end{matrix}\right.\\\left[{}\begin{matrix}x\le-\dfrac{1}{3}\\x\ge3\end{matrix}\right.\end{matrix}\right.\)

lời giải
a) \(\left\{{}\begin{matrix}-2x+\dfrac{3}{5}>\dfrac{2x-7}{3}\left(1\right)\\x-\dfrac{1}{2}< \dfrac{5\left(3x-1\right)}{2}\left(2\right)\end{matrix}\right.\)
(1)\(\Leftrightarrow\)
\(\dfrac{3}{5}+\dfrac{7}{3}>\left(\dfrac{2}{3}+2\right)x\)
\(\dfrac{44}{15}>\dfrac{8}{3}x\) \(\Rightarrow x< \dfrac{44.3}{15.8}=\dfrac{11}{5.2}=\dfrac{11}{10}\)
Nghiêm BPT(1) là \(x< \dfrac{11}{10}\)
(2) \(\Leftrightarrow2x-1< 15x-5\Rightarrow13x>4\Rightarrow x>\dfrac{4}{13}\)
Ta có: \(\dfrac{4}{13}< \dfrac{11}{10}\) => Nghiệm hệ (a) là \(\dfrac{4}{13}< x< \dfrac{11}{10}\)

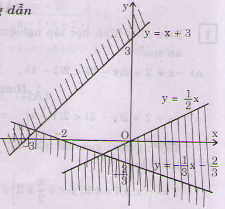
a) <=>
Miền nghiệm của hệ bất phương trình là miền không bị gạch sọc ở hình bên (không kể các điểm).
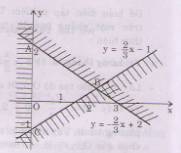
b) <=>
Miền nghiệm của hệ bất phương trình là miền tam giác ABC bao gồm cả các điểm trên cạnh AC và cạnh BC (không kể các điểm của cạnh AB).

|3x+4)/(x-2)| <=3
<=>|3 +10/(x-2) | <=3
10/(x-2) =t
<=> |3+t| <=3
9 +6t +t^2 <=9 <=> -6<=t <=0
10/(x-2) <=0 => x<2
10/(x-2) >=-6 <=>5/(x-2)>=-3
<=>5 <=-3(x-2) <=>3x <=10-5 =5 => x <=5/3
kết luận x<= 5/3
a) \(\left|\frac{3x+4}{x-2}\right|< =3̸\) đk: x\(\ne\) 2
BPT \(\Leftrightarrow\) \(\left\{{}\begin{matrix}\frac{3x+4}{x-2}\ge-3\\\frac{3x+4}{x-2}\le3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\frac{3x+4}{x-2}+3\ge0\\\frac{3x+4}{x-2}-3\le0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\frac{6x-2}{x-2}\ge0\\\frac{10}{x-2}\le0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\le\frac{1}{3}\\x>2\end{matrix}\right.\\x< 2\end{matrix}\right.\Rightarrow}x\le\frac{1}{3}}\)
b) \(\left|\frac{2x-1}{x-3}\right|\ge1\) đk: x\(\ne\) 3
BPT \(\Leftrightarrow\left[{}\begin{matrix}\frac{2x-3}{x-3}\le-1\\\frac{2x-3}{x-3}\ge1\end{matrix}\right.\)
ta có:
+) \(\frac{2x-3}{x-3}\le-1\Leftrightarrow\frac{2x-3}{x-3}+1\le0\Leftrightarrow\frac{3x-6}{x-3}\le0\Leftrightarrow2\le x< 3\)
+) \(\frac{2x-3}{x-3}\ge1\Leftrightarrow\frac{2x-3}{x-3}-1\ge0\Leftrightarrow\frac{x}{x-3}\ge0\Leftrightarrow\left[{}\begin{matrix}x\le0\\x>3\end{matrix}\right.\)
vậy tập nghiệm là: \((-\infty;0]\cup[2;3)\cup(3;+\infty)\)