Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{x-2}{2}+1\le\dfrac{x-1}{3}\)
\(\Leftrightarrow\dfrac{3\left(x-2\right)}{6}+\dfrac{1.6}{6}\le\dfrac{2\left(x-1\right)}{6}\)
`<=> 3x - 6 + 6 <= 2x-2`
`<=> 3x <= 2x-2`
`<=> 3x -2x <= -2`
`<=> x <= -2`
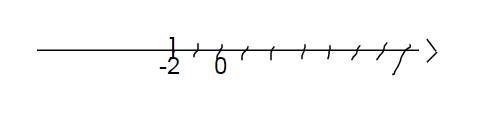
\(\dfrac{x-2}{2}\)+1≤\(\dfrac{x-1}{3}\)
<=>\(\dfrac{3x-6}{6}\)+\(\dfrac{6}{6}\)≤\(\dfrac{2x-1}{6}\)
<=>3x-6+6≤2x-1
<=>x<-1

=>2x^2-3x-4x+6+3x+8<2x^2+4x+2-4x
=>2x^2-4x+14<2x^2+2
=>-4x<-12
=>x>3

\(\Leftrightarrow3\left(1-2x\right)-2\left(x+1\right)< =6\)
=>3-6x-2x-2<=6
=>-8x+1<=6
=>-8x<=5
hay x>=5/8

`(x-2)/6 -(x-1)/3 < x/2`
`<=> (x-2)/6 -(2(x-1))/6 < (3x)/6`
`<=> x-2 - (2x-2) <3x`
`<=> x-2-2x+2<3x`
`<=> -x <3x`
`<=> -x-3x<0`
`<=> -4x<0`
`<=> x>0`
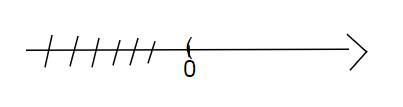

`(x+4)/5 - (x-2)/3 > 2`
`=> (3x+12 - 5x + 10)/15 > 2`
`=> 24 - 2x > 30`
`=> -2x > 6`
`=> x < -3`.

\(\dfrac{1-2x}{4}-2< \dfrac{1-5x}{8}\)
\(\Leftrightarrow\dfrac{2\left(1-2x\right)-16}{8}< \dfrac{1-5x}{8}\)
\(\Leftrightarrow2\left(1-2x\right)-16< 1-5x\)
\(\Leftrightarrow2-4x-16< 1-5x\)
\(\Leftrightarrow x< 15\)
Vậy \(S=\left\{x|x< 15\right\}\)

Ta có: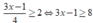 ⇔ 3x - 1 > 8
⇔ 3x - 1 > 8
⇔ 3x ≥ 9 ⇔ x ≥ 3
Vậy x ≥ 3 là nghiệm của bất phương trình.
Ta biểu diễn tập nghiệm trên trục số như sau: