Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1
a (9+x)=2 ta có (9+x)= 9+x khi 9+x >_0 hoặc >_ -9
(9+x)= -9-x khi 9+x <0 hoặc x <-9
1)pt 9+x=2 với x >_ -9
<=> x = 2-9
<=> x=-7 thỏa mãn điều kiện (TMDK)
2) pt -9-x=2 với x<-9
<=> -x=2+9
<=> -x=11
x= -11 TMDK
vậy pt có tập nghiệm S={-7;-9}
các cau con lai tu lam riêng nhung cau nhan với số âm thi phan điều kiện đổi chiều nha vd
nhu cau o trên mk lam 9+x>_0 hoặc x>_0
với số âm thi -2x>_0 hoặc x <_ 0 nha

Bài 1:
a. ||x|-2| = 1
1) ||x|-2| = |x-2| khi \(x\ge0\)
*) \(x-2\ge0\Leftrightarrow x\ge2\) . Với \(x\ge2\) ta có: \(x-2=1\Leftrightarrow x=3\)
*) \(x-2< 0\Leftrightarrow x< 2\) . Với x<2 ta có: \(-x+2=1\Leftrightarrow x=1\)
2) ||x| - 2| = |-x - 2| khi \(x< 0\)
*) \(-x-2\ge0\Leftrightarrow x\le-2\) . Với \(x\le-2\) ta có: \(-x-2=1\Leftrightarrow x=-3\)
*) \(-x-2< 0\Leftrightarrow x>-2\) . Với \(x>-2\) ta có: \(x+2=1\Leftrightarrow x=-1\)
vậy tập nghiệm của phương trình đã cho \(S=\left\{-3;-1;1;3\right\}\)
b. ||x|-1| = x+4
1) ||x|-1| = |x-1| khi \(x\ge0\)
*) \(x-1\ge0\Leftrightarrow x\ge1\) . Với \(x\ge1\) ta có: \(x-1=x+4\Leftrightarrow0x=5\) (vô nghiệm)
*) \(x-1< 0\Leftrightarrow x< 1\) . Với x<1 ta có: \(-x+1=x+4\Leftrightarrow x=-\dfrac{3}{2}\)
2) ||x|-1| = |-x-1| khi x<0
*) \(-x-1\ge0\Leftrightarrow x\le-1\) . Với \(x\le-1\) ta có: \(-x-1=x+4\Leftrightarrow x=-\dfrac{5}{2}\)
*) \(-x-1< 0\Leftrightarrow x>-1\) . Với x>-1 ta có: \(x+1=x+4\Leftrightarrow0x=3\) (vô nghiệm)
Vậy tập nghiệm của phương trình đã cho là \(S=\left\{-\dfrac{5}{2};-\dfrac{3}{2}\right\}\)
2)a)\(\left|2x+1\right|< \left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+1< x-3\\2x+1< -x+3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x-x< -1-3\\2x+x< -1+3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< -4\\3x< 2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -4\\x< \dfrac{2}{3}\end{matrix}\right.\)
Vậy S=...

\(\left|5-2x\right|=1-x\)
\(\orbr{\begin{cases}5-2x=1-x\\-5+2x=1-x\end{cases}\Rightarrow\orbr{\begin{cases}5-2x-1+x=0\\-5+2x-1+x=0\end{cases}\Rightarrow}\orbr{\begin{cases}4-x=0\\-6+3x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=4\\3x=6\end{cases}\Rightarrow}\orbr{\begin{cases}x=4\\x=2\end{cases}}}\)

a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
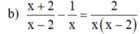
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
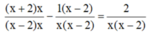
![]()
![]()
![]()
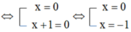
![]()
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}

a: =>9x^2+6x+1-6(2x^2-13x+21)=0
=>9x^2+6x+1-12x^2+78x-126=0
=>-3x^2+84x-125=0
=>\(x\in\left\{26.42;1.58\right\}\)
b: =>(3x+1)[(2x-5)^2-(x-3)^2]=0
=>(3x+1)(2x-5-x+3)(2x-5+x-3)=0
=>(3x+1)(x-2)(3x-8)=0
=>\(x\in\left\{-\dfrac{1}{3};2;\dfrac{8}{3}\right\}\)
c; =>(x+5)(0,75x-3+1,25x)=0
=>(x+5)(2x-3)=0
=>x=3/2 hoặc x=-5