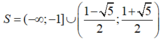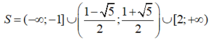giải bất phương trình :2x2 + 3x nhỏ hơn hoặc bằng 0

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TK

Trần Kim Ngân

21 tháng 2 2021 - olm

giải bất phương trình :

2x² + 3x nhỏ hơn hoặc bằng 0

#Toán lớp 10

1

VT

Vũ Thị Thúy

22 tháng 2 2021

Đáp án là -3/2

Các câu hỏi dưới đây có thể giống với câu hỏi trên

DN

dũng nguyễn tiến

18 tháng 1 2022

tìm tất cả giá trị của m để bất phương trình -2x2 +<m-1>x+m2-1 < hoặc bằng 0 có nghiệm đúng với xϵR

#Toán lớp 10

1

E

Eren

18 tháng 1 2022

a = -2 < 0 rồi, xét Δ không dương nữa là xong

PT

Pham Trong Bach

9 tháng 9 2017

Tập nghiệm của bất phương trình 2 x 2 - 3 x + 1 4 x - 3 < 0 là A. 1 2 ; 3 4 ∪ 3 4 ; 1 B. 1 2 ; 3 4 ∩ 3 4 ; 1 C. S = 1 2 ; 1 D. S = - ∞ ; 1 2 ...

#Toán lớp 10

1

CM

Cao Minh Tâm

9 tháng 9 2017

PT

Pham Trong Bach

2 tháng 7 2017

Điều kiện của bất phương trình 2 x + 3 5 - x + 2 x 2 - 3 x + 1 > 0 là: A. [ x ≥ 1 x ≤ 1 2 B. [ 1 ≤ x ≤ 5 x ≤ 1 2 C. [ 1 ≤ x < 5 x ≤ 1 2 ...

#Toán lớp 10

1

CM

Cao Minh Tâm

2 tháng 7 2017

Chọn C.

Điều kiện xác định của bất phương trình là:

Đề thi Học kì 2 Toán 10 có đáp án (Đề 3)

Đề thi Học kì 2 Toán 10 có đáp án (Đề 3)

LT

Lý Tuệ Minh

12 tháng 3 2022

giải bất phương trình sau (2 x + 6) (x^2 + x +1)\5x^2-3x-2 > hoặc = 0

#Toán lớp 10

1

TH

Thanh Hoàng Thanh

12 tháng 3 2022

undefined

PT

Pham Trong Bach

17 tháng 7 2017

Giải bất phương trình sau: x 2 - x - 2 x 2 - x - 1 ≥ 0 A. B. C. ...

#Toán lớp 10

1

CM

Cao Minh Tâm

17 tháng 7 2017

Chọn D

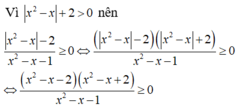
Bảng xét dấu

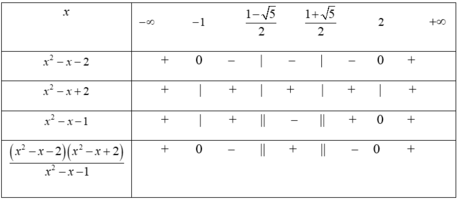
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là

PT

Pham Trong Bach

20 tháng 11 2019

Giải thích vì sao cặp bất phương trình sau tương đương? 2x2 + 5 ≤ 2x - 1 và 2x2 - 2x + 6 ≤ 0

#Toán lớp 10

1

CM

Cao Minh Tâm

20 tháng 11 2019

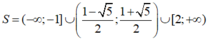
Ta có:

2x2 + 5 ≤ 2x – 1

⇔ 2x2 + 5 + 1 – 2x ≤ 2x – 1 + 1 – 2x (Cộng cả hai vế của BPT với 1 – 2x).

⇔ 2x2 – 2x + 6 ≤ 0.

Vậy hai BPT đã cho tương đương: 2x2 + 5 ≤ 2x – 1 ⇔ 2x2 – 2x + 6 ≤ 0.

MK

MINH KHÔI

13 tháng 8 2021 - olm

1. trong mặt phẳng tọa độ Oxy, phương trình đường thẳng đi qua điểm M (2;3) và có véc tơ pháp tuyến n = (2;7) là2. cho tam giác ABC có AB = 2, ac = 3, BAC = 120 độ. Độ dài cạnh BC bằng?3. Tập nghiệm của bất phương trình -2x2 + 3x +2 lớn hơn hoặc bằng 0 là?4. Tìm trên đường tròn có bán kính R = 3, độ dài cung có số đo 30 độ là bao nhiêu? 5. Viết phương trình tổng quát của đường thẳng đi qua...

#Toán lớp 10

2

NV

Nguyễn Văn Lâm ( ✎﹏IDΣΛ亗 )

14 tháng 8 2021

\(3.\)

\(-2x^2+3x+2\ge0\)

\(\Leftrightarrow-\left(x-2\right)\left(2x+1\right)\ge0\)

\(\Leftrightarrow\left(2-x\right)\left(2x+1\right)\ge0\)

Giải bất phương trình ra được: \(\frac{-1}{2}\le x\le2\)

Vậy \(x\in\left\{\frac{-1}{2};2\right\}\)

NV

Nguyễn Văn Lâm ( ✎﹏IDΣΛ亗 )

14 tháng 8 2021

\(5.\)

Đường thẳng đã cho song song với đường thẳng \(2x+y+2020=0\)

<=> Đường thẳng đã cho có véc tơ pháp tuyến là \(n\left(2;1\right)\)

Mà đường thẳng đã cho đi qua \(M\left(3;0\right)\)nên ta có phương trình:

\(2\left(x-3\right)+y=0\)

\(2x+y-6=0\)

PH

Phạm Huỳnh Hoài Thương

9 tháng 3 2023

Giúp vs ạBài 1 giải các bất phương trình saua.x2 - x - 6 = 0b.2x2 - 7x + 5 < 0c.3x2 - 9x + 6 ≥ 0d.2x2 - 5x + 3 < 0Bài 2 Giải phương trình sauA.√x2 + x + 5 = √2x2 - 4x + 1B.√11x2 -14x - 12 = √3x2 + 4x -...

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 3 2023

Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

PT

Pham Trong Bach

25 tháng 11 2018

Giải bất phương trình: x 2 + 10 ≤ 2 x 2 + 1 x 2 - 8 A. B. C. ...

#Toán lớp 10

1

CM

Cao Minh Tâm

25 tháng 11 2018

Chọn C

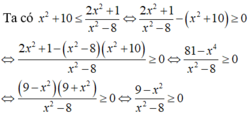
Lập bảng xét dấu

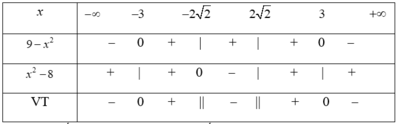
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là