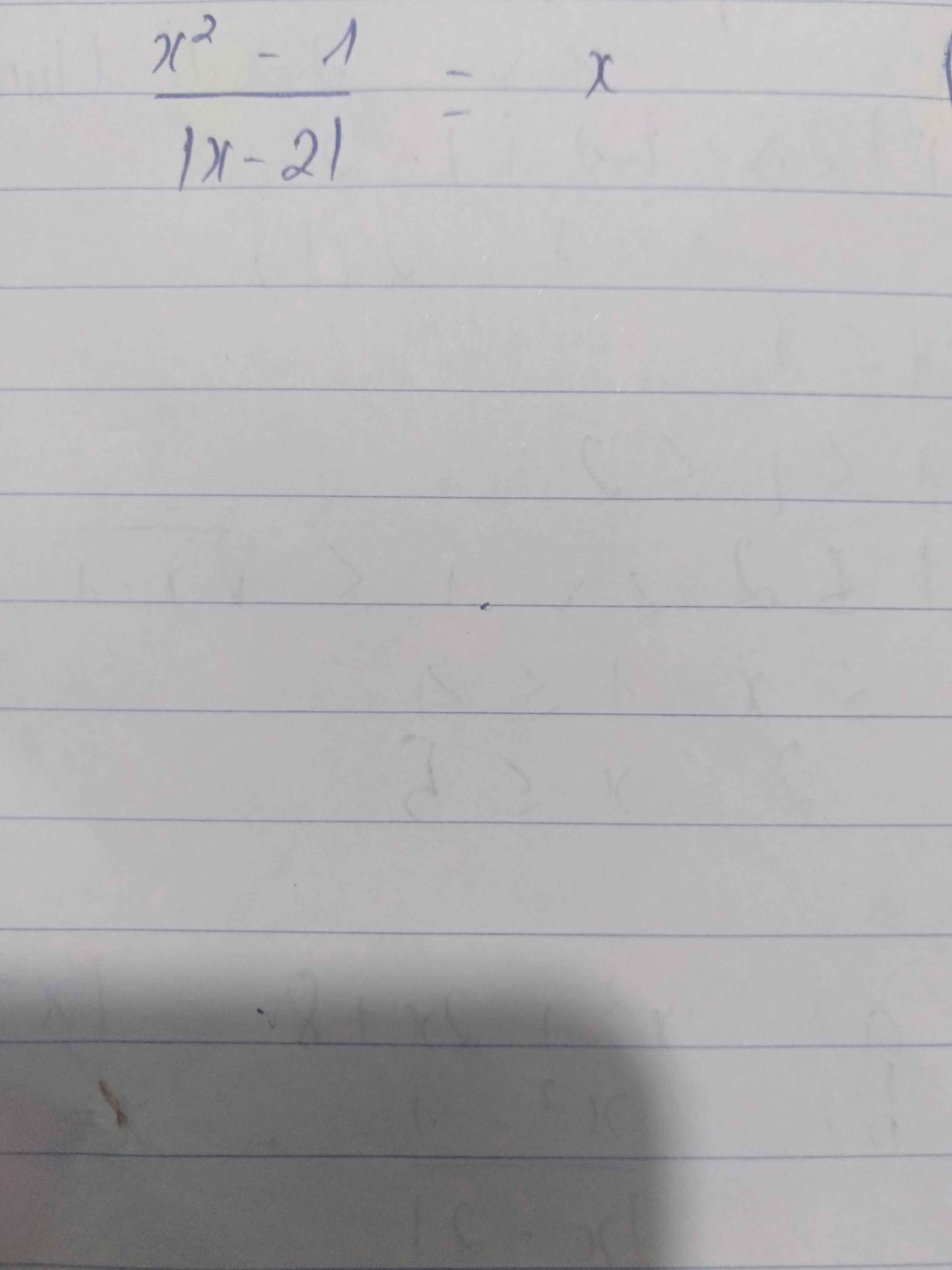Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M(x,y) là điểm cần tìm
\(\overrightarrow{MA}+\overrightarrow{MB}=(-1-2x;8-2y)\)
\(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=(8-3x;16-3y)\)
Theo giả thiết \(3|\overrightarrow{MA}+\overrightarrow{MB}|=2|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}|\), suy ra
\(3\sqrt{(-1-2x)^2+(8-2y)^2}=2\sqrt{(8-3x)^2+(16-3y)^2}\)
\(\Leftrightarrow 9(4x^2+4y^2+4x-32y+65)=4(9x^2+9y^2-48x-96y+320)\)
\(\Leftrightarrow 228x+96y-695=0\)
Vậy tập các điểm M cần tìm là đường thẳng 228x+96y-695=0


2. \(|x| +|x-1| ≤ 5 \\ \Leftrightarrow |x| + |x-1| ≤ \dfrac{5}{2}\)
| \(-∞\) | \(0\) | \(1\) | \(+∞\) | |
| \(|x|\) | \(-x\) | \(x\) | \(x\) | \(x\) |
| \(|x-1|\) | \(1-x\) | \(1-x\) | \(x-1\) | \(x-1\) |
| \(|x|+|x-1|\) | \(1-2x\) | \(1\) | \(2x-1\) | \(2x-1\) |
TH1: \(1-2x ≤ \dfrac{5}{2} \Leftrightarrow x ≥ \dfrac{-3}{4}\)
TH2: \(2x-1 ≤ \dfrac{5}{2} \Leftrightarrow x ≤ \dfrac{7}{4}\)
Vậy....

Giá trị tuyệt đối của một số là khoảng cách của số đó đến điểm 0 trên trục số nằm ngang.
|0| = 0; |1,25| = 1,25;
|(-3)/4| = 3/4; |-π| = π


Lời giải:
ĐKXĐ: $x\neq 2$
PT $\Rightarrow x^2-1=x|x-2|$
Nếu $x>2$ thì pt trở thành: $x^2-1=x(x-2)=x^2-2x$
$\Leftrightarrow x=\frac{1}{2}< 2$ (loại)
Nếu $x< 2$ thì pt trở thành: $x^2-1=x(2-x)=2x-x^2$
$\Leftrightarrow 2x^2-2x-1=0$
$\Rightarrow x=\frac{1\pm \sqrt{3}}{2}$ (đều tm)

Đáp án A
Ta có các sai số tuyệt đối là:
∆ a = 2 7 - 0 , 28 = 1 175 ; ∆ b = 2 7 - 0 , 29 = 3 700 ; ∆ c = 2 7 - 0 , 286 = 1 3500 .