Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`[2-x]/x >= 1`
`<=>[2-x-x]/x >= 0`
`<=>[2-2x]/x >= 0`
`<=>0 < x <= 1`
`->\bb B`

\(-\dfrac{1}{2}x+6< 0\Leftrightarrow-\dfrac{1}{2}x< -6\Leftrightarrow\cdot\dfrac{1}{2}x>6\Leftrightarrow x>12\)
(sai thì thoi nha)
\(-\dfrac{1}{2}x+6< 0\)
\(\Leftrightarrow-\dfrac{1}{2}x< -6\)
\(\Leftrightarrow x>\left(-6\right):\left(-\dfrac{1}{2}\right)\)
\(\Leftrightarrow x>12\)
--> Chọn A

\(5x-1>2x+3\)
\(\Leftrightarrow5x-2x>3+1\)
\(\Leftrightarrow3x>4\)
\(\Leftrightarrow x>\dfrac{4}{3}\)
--> Chọn C

Vẽ đồ thị:
- Vẽ đồ thị hàm số y = f(x) = x + 1 qua hai điểm (0; 1) và (-1; 0).
- Vẽ đồ thị hàm số y = g(x) = 3 - x qua hai điểm (0; 3) và (3; 0)
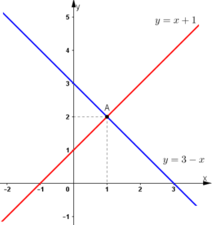
a) Nghiệm của phương trình f(x) = g(x) chính là hoành độ giao điểm của hai đường thẳng y = f(x) và y = g(x).
Giao điểm của hai đường thẳng y = x + 1 và y = 3 – x là điểm A(1; 2).
Do đó phương trình f(x) = g(x) có nghiệm x = 1.
Kiểm tra bằng tính toán:
f(x) = g(x) ⇔ x + 1 = 3 - x ⇔ 2x = 2 ⇔ x = 1.
b) Khi x > 1 thì đồ thị hàm số y = f(x) nằm phía trên đồ thị hàm số y = g(x), hay với x > 1 thì f(x) > g(x).
Kiểm tra bằng tính toán:
f(x) > g(x) ⇔ x + 1 > 3 - x ⇔ 2x > 2 ⇔ x > 1.
c) Khi x < 1 thì đồ thị hàm số y = f(x) nằm phía dưới đồ thị hàm số y = g(x), hay với x < 1 thì f(x) < g(x).
Kiểm tra bằng tính toán:
f(x) < g(x) ⇔ x + 1 < 3 - x ⇔ 2x < 2 ⇔ x < 1.

1.
\(2x+1\ge0\Rightarrow x\ge-\dfrac{1}{2}\)
Khi đó pt đã cho tương đương:
\(x^2+2x+2m=\left(2x+1\right)^2\)
\(\Leftrightarrow x^2+2x+2m=4x^2+4x+1\)
\(\Leftrightarrow3x^2+2x+1=2m\)
Xét hàm \(f\left(x\right)=3x^2+2x+1\) trên \([-\dfrac{1}{2};+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}< -\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{2}\right)=\dfrac{3}{4}\) ; \(f\left(\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi \(\dfrac{2}{3}< 2m\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}< m\le\dfrac{3}{8}\)
\(\Rightarrow P=\dfrac{1}{8}\)
3.
Đặt \(x^2=t\ge0\Rightarrow\left[{}\begin{matrix}x=\sqrt{t}\\x=-\sqrt{t}\end{matrix}\right.\)
Pt trở thành: \(t^2-3mt+m^2+1=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=9m^2-4\left(m^2+1\right)>0\\t_1+t_2=3m>0\\t_1t_2=m^2+1>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{2}{\sqrt{5}}\)
Ta có:
\(M=x_1+x_2+x_3+x_4+x_1x_2x_3x_4\)
\(=-\sqrt{t_1}-\sqrt{t_2}+\sqrt{t_1}+\sqrt{t_2}+\left(-\sqrt{t_1}\right)\left(-\sqrt{t_2}\right)\sqrt{t_1}.\sqrt{t_2}\)
\(=t_1t_2=m^2+1\) với \(m>\dfrac{2}{\sqrt{5}}\)
`[2-x]/[x+3] > x+1` `ĐK: x \ne -3`
`=>` Loại đ/á `\bb A`
Thay `x=-1` vào bất ptr có: `1,5 > 0` (Luôn đúng) `->\bb B` t/m
Thay `x=2` vào bất ptr có: `0 > 3` (Vô lí) `->\bb C` loại
Thay `x=0` vào bất ptr có: `2/3 > 1` (Vô lí) `->\bb D` loại
______________________________________________________
`=>` Chọn `\bb B`