
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-y^2-2y-1\)
\(=x^2-\left(y+1\right)^2\)
\(=\left(x-y-1\right)\left(x+y+1\right)\)
\(=100\cdot\left(93-6-1\right)\)
=8600

\(Q=x^2-y^2-2y-1\)
\(\Rightarrow Q=x^2-\left(y^2+2y+1\right)\)
\(\Rightarrow Q=x^2-\left(y+1\right)^2\)
\(\Rightarrow Q=\left(x-y-1\right)\left(x+y+1\right)\)
Thay \(x=93;y=6\)vào \(Q\)ta được :
\(Q=\left(93-6-1\right)\left(93+6+1\right)\)
\(\Rightarrow Q=86.100\)
\(\Rightarrow Q=8600\)
Vậy \(Q=8600\)


a) x2−y2−2y−1x2−y2−2y−1 tại x=93x=93 và y=6y=6
Ta có : x2−y2−2y−1=x2−(y2+2y+1)x2−y2−2y−1=x2−(y2+2y+1)
=x2−(y+1)2=x2−(y+1)2
=(x−y−1)(x+y+1)=(x−y−1)(x+y+1)
Khi x=93x=93 và y=6y=6 , ta có :
(93−6−1)(93+6+1)(93−6−1)(93+6+1) =86.100=86.100
=8600

\(a,=5\left(x^2+2xy+y^2\right)-10y^2+5=5\left(x+y\right)^2-10y^2+5\\ =5\left(1+2\right)^2-10\cdot4+5=45-40+5=10\\ b,=7\left(x-y\right)-\left(x-y\right)^2=\left(x-y\right)\left(7-x+y\right)\\ =\left(2-2\right)\left(7-2+2\right)=0\)
b: \(=7\left(x-y\right)-\left(x-y\right)^2\)
\(=\left(x-y\right)\left(7-x+y\right)=0\)

Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$
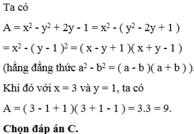
=(x-y-1)(x+y+1)
=100x86=8600