Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C.
Gợi ý: Xem lại công thức của phương trình bậc hai.

Đáp án: D
z ∈ R ⇔ z = z , ( z 1 + z 2 )= z 1 + z 2 , ( z 1 . z 2 )= z 1 . z 2

Đáp án: D.
z ∈ R ⇔ z = z , (z1 + z 2 ) = z 1 + z 2 , (z1. z 2 ) = z−1. z 2 .

Cách 1 :
Phương trình a z 2 + bz + c = 0 có Δ = b 2 - 4ac
+ TH1 : Δ < 0, phương trình có hai nghiệm phức 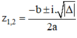
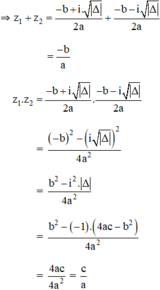
+ TH2: Δ ≥ 0, theo định lý Vi-et ta có:
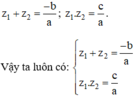
Cách 2 :

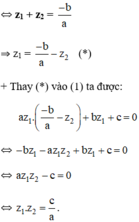

Đặt \(z_1=x+yi\Rightarrow z_2=x-yi\)
\(\Rightarrow z_1z_2=x^2+y^2\)
\(\left|z_1^2\right|+\left|z_2^2\right|=10\Leftrightarrow\left|\left(x+yi\right)^2\right|+\left|\left(x-yi\right)^2\right|=10\)
\(\Leftrightarrow\left|x^2-y^2+2xyi\right|+\left|x^2-y^2-2xyi\right|=10\)
\(\Leftrightarrow\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}+\sqrt{\left(x^2-y^2\right)^2+4x^2y^2}=10\)
\(\Leftrightarrow\left(x^2-y^2\right)^2+4x^2y^2=25\)
\(\Leftrightarrow\left(x^2+y^2\right)^2=25\)
\(\Leftrightarrow x^2+y^2=5\)


Đáp án: C.
Gợi ý: Xem lại công thức của phương trình bậc hai.