Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp:
+) Từ giả thiết ![]() , tìm ra đường biểu diễn (C) của các số phức z.
, tìm ra đường biểu diễn (C) của các số phức z.
+) Gọi A, B lần lượt là điểm biểu diễn của ![]()
![]() vị trí của AB đối với đường tròn (C).
vị trí của AB đối với đường tròn (C).
![]()
+) Sử dụng công thức trung tuyến tính O A 2 + O B 2
+) Sử dụng BĐT Bunhiascopsky tìm GTLN của OA+OB
Cách giải:
Ta có: ![]()
với ![]()
![]()
![]() M(x;y) biểu diễn z thuộc đường tròn tâm I(
1
;
2
)bán kính R=1.
M(x;y) biểu diễn z thuộc đường tròn tâm I(
1
;
2
)bán kính R=1.
Lại có: ![]()
Mặt khác theo công thức trung tuyến ta có:
![]()
Theo BĐT Bunhiascopsky ta có:
![]()

Đáp án D.
Ta có: ![]()
![]()
![]()
=> M(x;y) biểu diễn z thuộc đường tròn tâm I(1; 2 ) bán kính R = 1
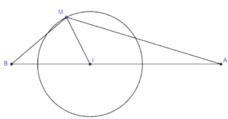
Giả sử ![]() => AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
=> AB = 2 = 2R nên B là đường kính của đường tròn (I;R)
Lại có: | z 1 | + | z 2 | = OA + OB
Mặt khác theo công thức trung tuyến ta có:
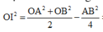
![]()
Theo BĐT Bunhiascopky ta có: ![]()
![]()

Đáp án C
HD: Ta có
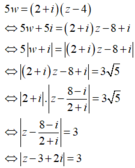
![]() Tập hợp điểm M(z) là đường tròn
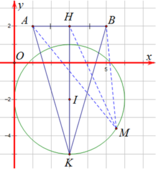
Tập hợp điểm M(z) là đường tròn ![]() tâm I(3;-2), R=3.
tâm I(3;-2), R=3.
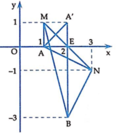
Gọi A(1;2), B(5;2) và E(3;2) là trung điểm của AB suy ra P=MA+MB
Lại có
![]()
![]() P lớn nhất
P lớn nhất  ME lớn nhất.
ME lớn nhất.
Mà ![]()
Vậy ![]()

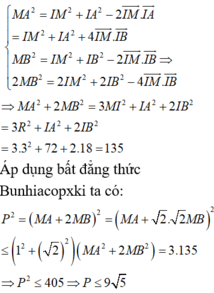




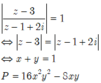
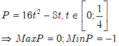




Đáp án D