Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Sau 1 chu kì bán rã: 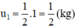
Sau 2 chu kì bán rã: 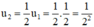
Sau 3 chu kì bán rã: 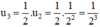
…
Tổng quát : Sau n chu kì bán rã : 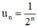
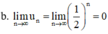
c. Chất phóng xạ không còn độc hại nữa khi khối lượng chất phóng xạ còn lại < 10-6 g = 10-9 kg
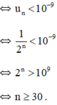
Vậy sau 30 chu kì = 30.24000 = 720 000 năm thì 1kg chất phóng xạ này không còn độc hại nữa.

a) Với \({M_0} = 200,T = 9,M\left( t \right) = 100\) ta có:
\(100 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{2} \Leftrightarrow \frac{t}{9} = 1 \Leftrightarrow t = 9\)
Vậy sau 9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 100 g.
b) Với \({M_0} = 200,T = 9,M\left( t \right) = 50\) ta có:
\(50 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{4} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = {\left( {\frac{1}{2}} \right)^2} \Leftrightarrow \frac{t}{9} = 2 \Leftrightarrow t = 18\)
Vậy sau 18 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.
c) Với \({M_0} = 200,T = 9,M\left( t \right) = 20\) ta có:
\(20 = 200{\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} \Leftrightarrow {\left( {\frac{1}{2}} \right)^{\frac{t}{9}}} = \frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _{\frac{1}{2}}}\frac{1}{{10}} \Leftrightarrow \frac{t}{9} = {\log _2}10 \Leftrightarrow t = 9{\log _2}10 \approx 29,9\)
Vậy sau 29,9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.

a) Nhận xét: u1 = ; u2 =
; u3 =
; ... un =
.
Điều này chứng minh đơn giản bằng quy nạp.
b) lim un = lim ()n= 0 = vì lim qn = 0 nếu |q| < 1.
c) Đổi 10-6 g = .
kg =
kg.
Muốn có un = <
, ta cần chọn n0 sao cho 2n0 > 109. Chẳng hạn, với n0 = 36, thì
236 = (24)9 = 16 9 > 109. Nói cách khác, sau chu kì thứ 36 (nghĩa là sau 36.24000 = 864 000 (năm), chúng ta không còn lo lắng về sự độc hại của khối lượng chất phóng xạ còn lại.

a, Khối lượng polonium-210 còn lại sau 2 năm là:
\(M\left(730\right)=100\cdot\left(\dfrac{1}{2}\right)^{\dfrac{730}{138}}\approx1,92\left(g\right)\)
b, Ta có:
\(M\left(t\right)=40\\ \Leftrightarrow40=100\cdot\left(\dfrac{1}{2}\right)^{\dfrac{t}{138}}\\ \Leftrightarrow\left(\dfrac{1}{2}\right)^{\dfrac{t}{138}}=\dfrac{4}{10}\\ \Leftrightarrow\dfrac{t}{138}=log_{\dfrac{1}{2}}\left(\dfrac{4}{10}\right)\\ \Leftrightarrow t=138\cdot log_{\dfrac{1}{2}}\left(\dfrac{4}{10}\right)\approx182,43\)
Vậy sau 183,43 ngày thì còn lại 40g polonium-210.

Dãy số chỉ khối lượng còn lại của 20 gam poloni 210 sau \(n\) chu kì là một cấp số nhân có số hạng đầu \({u_1} = 20\) và công bội \(q = \frac{1}{2}\).
a) Sau 690 ngày thì số chu kì bán rã thực hiện được là: \(690:138 = 5\) (chu kì).
Vậy khối lượng còn lại của 20 gam poloni 210 là: \({u_5} = {u_1}.{q^4} = 20.{\left( {\frac{1}{2}} \right)^4} = 1,25\) (gam).
b) Sau 7314 ngày thì số chu kì bán rã thực hiện được là: \(7314:138 = 53\) (chu kì).
Vậy khối lượng còn lại của 20 gam poloni 210 là: \({u_{53}} = {u_1}.{q^{52}} = 20.{\left( {\frac{1}{2}} \right)^{52}} \approx 44,{4.10^{ - 16}}\) (gam).

a: Nhiệt độ ban đầu là:
\(T=25+70\cdot e^{-0.5\cdot0}=95\left(^0C\right)\)
b: ĐặtT=30
=>\(25+70\cdot e^{-0.5t}=30\)
=>\(e^{-0.5t}=\dfrac{1}{14}\)
=>\(-0.5t=ln\left(\dfrac{1}{14}\right)\)
=>\(t\simeq5,28\simeq6\)
=>Sau 6 phút thì nhiệt độ còn lại tầm 30 độ C

tham khảo
a) Khối lượng vi khuẩn tại thời điểm bắt đầu nuôi cấy là:
\(M\left(0\right)=50.1,06^0=50\left(g\right)\)
b) Khối lượng vi khuẩn sau \(2\) giờ là:
\(M\left(2\right)=50.1,06^2=56,18\left(g\right)\)
Khối lượng vi khuẩn sau \(10\) giờ là:
\(M\left(10\right)=50.1,06^{10}\approx89,54\left(g\right)\)
c) Xét hàm số \(M\left(t\right)=50.1,06^t\).
Vì \(1,06>1\) nên hàm số \(M\left(t\right)=50.1,06^t\) là hàm số đồng biến. Vậy khối lượng vi khuẩn tăng dần theo thời gian.

a) Sau một chu kì bán rã \({u_1} = 1.\frac{1}{2} = \frac{1}{2}\left( {kg} \right)\)
Sau hai chu kì bán rã \({u_2} = \frac{1}{2}.{u_1} = \frac{1}{{{2^2}}}\left( {kg} \right)\)
…
Vậy sau n chu kì bán rã \({u_n} = \frac{1}{{{2^n}}}\)
b) \(\lim {u_n} = \lim \frac{1}{{{2^n}}} = \lim {\left( {\frac{1}{2}} \right)^n} = 0\)
c) Đổi \({10^{ - 6}}g = {10^{ - 9}}kg\)
Vì chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \({10^{ - 6}}\) g nên ta có
\({u_n} < {10^{ - 9}} \Leftrightarrow \frac{1}{{{2^n}}} < {10^{ - 9}} \Leftrightarrow {2^n} > {10^9} \Leftrightarrow n > {\log _2}{10^9} \approx 29,9\)
Vậy sau 30 chu kì là 30.24 000 = 720 000 năm thì khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.

Phương trình gia tốc là: \(a\left(t\right)=v'\left(t\right)=2t+2\)
a, Tại thời điểm t = 3(s), gia tốc tức thời là: \(a\left(3\right)=2\cdot3+2=8\left(m/s^2\right)\)
b, Vận tốc của chất điểm bằng 8
\(\Rightarrow t^2+2t-8=0\\ \Leftrightarrow\left(t-2\right)\left(t+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}t=2\\t=-4\left(loại\right)\end{matrix}\right.\)
Vậy khi t = 8s thì chất điểm đạt vận tốc 8m/s.
a: Khối lượng của vật thời điểm t=0 là: \(m\left(0\right)=13\cdot e^{-0.015\cdot0}=13\left(kg\right)\)
b: Sau 45 ngày khối lượng còn lại là;
\(m\left(45\right)=13\cdot e^{-0.015\cdot45}\simeq6,62\left(kg\right)\)