Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

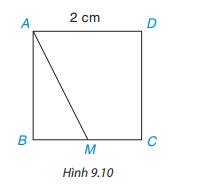
a) Đường vuông góc kẻ từ A đến BC là: AB
Đường xiên kẻ từ A đến BC là: AM
b) AB < AM (Trong các đường xiên và đường vuông góc kẻ từ 1 điểm nằm ngoài 1 đường thẳng đến đường thẳng đó thì đường vuông góc là đường ngắn nhất.)
c) Vì CB \( \bot \) AB nên khoảng cách từ C đến AB là độ dài CB = 2 cm

a/ Vì AH là tia p/g của \(\widehat{BAC}\) (gt)
=> \(\widehat{BAH}=\widehat{CAH}=\frac{60^o}{2}=30^o\)
Vậy \(\widehat{BAH}=30^o\)
b/ Xét ΔAHB và ΔAHK có:
AH: Cạnh chung
\(\widehat{BAH}=\widehat{CAH}\) (AH là tia p/g của \(\widehat{BAC}\) (gt))
AB = AK (gt)
=> ΔAHB = ΔAHK(c.g.c)(đpcm)
c/ Vì ΔAHB = ΔAHK (ý b)
=> \(\widehat{AHB}=\widehat{AHK}\) (2 góc tương ứng)
mà \(\widehat{AHB}+\widehat{AHK}=180^o\) (kề bù)
=> \(\widehat{AHB}=\widehat{AHK}=\frac{180^o}{2}=90^o\)
=> AH \(\perp\) BK (đpcm)
d/ Xét ΔAHN và ΔAHQ có:
\(\widehat{AHN}=\widehat{AHQ}=90^o\left(gt\right)\)
AH: Cạnh chung
\(\widehat{BAH}=\widehat{CAH}\) (AH là p/g của \(\widehat{BAC}\) (gt))
=> ΔAHN = ΔAHQ(g.c.g)
=> HN = HQ(2 cạnh tương ứng) (1)
mà \(\widehat{AHN}=\widehat{AHQ}=90^o\left(gt\right)\Rightarrow AH\perp QN\) (2)
Từ (1) và (2)
=> AH là đường trung trực của QN (đpcm)

a: Xét ΔABC có \(\widehat{B}>\widehat{C}\)
nên AB<AC
Xét ΔABC có AB<AC
mà HB là hình chiếu của AB trên BC
và HC là hình chiếu của AC trên BC
nên HB<HC
b: Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BA=BD
BH chung
Do đó: ΔAHB=ΔDHB
c: Xét ΔBAC và ΔBDC có
BA=BD
\(\widehat{ABC}=\widehat{DBC}\)
BC chung
DO đó: ΔBAC=ΔBDC
Suy ra: \(\widehat{BAC}=\widehat{BDC}=90^0\)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>góc BAH=góc CAH=50/2=25 độ
c: góc AKC=góc AHC=90 độ
=>AKHC nội tiếp
=>góc KAH=góc KCH

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
Suy ra: \(\widehat{BAH}=\widehat{CAH}\)
hay AH là tia phân giác của góc BAC
b: \(\widehat{BAC}=70^0\)
nên \(\widehat{BAH}=35^0\)
=>\(\widehat{B}=55^0\)
=>BH<AH
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra: AD=AE
hay ΔADE cân tại A

Câu hỏi của Lê Thu Phương Anh - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.
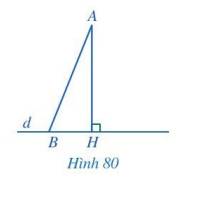
a) Tổng ba góc trong một tam giác bằng 180°. Mà góc H bằng 90° nên tổng hai góc còn lại trong tam giác bằng \(180^\circ - 90^\circ = 90^\circ \).
Vậy \(\widehat {AHB} > \widehat {ABH}\).
b) Cạnh đối diện với góc lớn hơn thì có độ dài lớn hơn. Vậy AB > AH (AB đối diện với góc H; AH đối diện với góc B).