K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 6 2020
10.
\(log_2\left(x^2-2x+3\right)>1\Leftrightarrow x^2-2x+3>2\)
\(\Leftrightarrow x^2-2x+1>0\)
\(\Leftrightarrow\left(x-1\right)^2>0\)
\(\Leftrightarrow x\ne1\)
11.
\(\int\limits^{10}_4f\left(x\right)dx=\int\limits^{10}_0f\left(x\right)dx-\int\limits^4_0f\left(x\right)dx=6\)
12.
\(\int\limits^{100}_0\left(1+f\left(x\right)\right)dx=\int\limits^{100}_0dx+\int\limits^{100}_0f\left(x\right)dx=100+3=103\)
13.
\(\int\limits^9_0\left[f\left(x\right)+2x\right]dx=\int\limits^9_0f\left(x\right)dx+\int\limits^9_02xdx=5+81=86\)
14.
\(\overline{z}=-6i-3i^2=3-6i\Rightarrow z=3+6i\)
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 6 2020
5.
\(\lim\limits_{x\rightarrow\infty}\frac{2x+1}{3x-1}=\frac{2}{3}\Rightarrow\left\{{}\begin{matrix}m=2\\n=3\end{matrix}\right.\)
\(\Rightarrow2m-n=1\)
6.
Đáp án C đúng, đồ thị hàm số chỉ có 1 TCN \(y=5\)
7.
\(\lim\limits_{x\rightarrow\infty}\left(\frac{x-3}{1-x}-2\right)=\frac{1}{-1}-2=-3\)
\(\Rightarrow y=-3\) là tiệm cận ngang
8.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2+2x+3}=0\Rightarrow y=0\) là TCN
9.
\(\lim\limits_{x\rightarrow+\infty}y=\lim\limits_{x\rightarrow+\infty}\frac{2x+3}{\sqrt{x^2+2x+3}+x}=\lim\limits_{x\rightarrow+\infty}\frac{2+\frac{3}{x}}{\sqrt{1+\frac{2}{x}+\frac{3}{x^2}}+1}=\frac{2}{1+1}=1\)
\(\lim\limits_{x\rightarrow-\infty}y=+\infty\)
Đồ thị có 1 TCN là \(y=1\)
27 tháng 9 2016
Ta có hình vẽ:
Ta có:
góc aAC = góc B + C
góc bCc = góc A + B
góc cAB = góc B + C
góc b'BA = góc A + C
góc c'CB = góc A + B
góc a'BC = góc A + C
Công theo vế ta được tổng 6 góc ngoài của tam giác ABC = 4 x (A + B + C)
= 4 x 180o
= 720o
28 tháng 9 2016
Tú Tự Ti: 360o là tổng 3 góc ngoài của tam giác c` tổng các góc ngoài (6 góc) là 720o
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 9 2021
Công thức tính nhanh phương trình đường thẳng qua 2 cực trị của hàm bậc 3 dạng: \(y=ax^3+bx^2+cx+d\) là: \(y=\left(\dfrac{2c}{3}-\dfrac{2b^2}{9a}\right)x+\left(d-\dfrac{bc}{9a}\right)\)
Đường thẳng đi qua gốc tọa độ (2 cực trị thẳng hàng O) khi tung độ gốc bằng 0
\(\Rightarrow d-\dfrac{bc}{9a}=0\)
Áp dụng cho bài này:
\(3-\dfrac{\left(-2\right).m}{9.\dfrac{1}{3}}=0\Rightarrow-2m=9\Rightarrow m=-\dfrac{9}{2}\in\left(-5;-3\right)\)
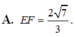
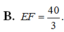
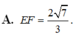
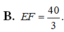
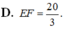
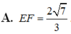
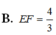
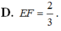
Đề lỗi rồi. Bạn xem lại.