Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1 (2đ) a) √25–√494+√0,2525–494+0,25
b) (–2527–3142)–(–727–342)(–2527–3142)–(–727–342)
c) 10310–(9,5–0,25.18):0,5115–11210310–(9,5–0,25.18):0,5115–112
d) 349.192–349.52–(120–14)2.(–12–19314)349.192–349.52–(120–14)2.(–12–19314)
Bài 2 (2đ)
1) Tìm x biết:
a) ∣∣∣12x–16∣∣∣=13|12x–16|=13
b) (4x2–3)3+8=0(4x2–3)3+8=0
2) Vẽ đồ thị hàm sốy=–12xy=–12x. Từ đó chứng minh 3 điểm A(2; -1), B(-12; -6) và C(-2; 1) không thẳng hàng.
Bài 3 (1,5đ) Có ba máy bơm cùng bơm nước vào ba bể có thể tích bằng nhau (lúc đầu các bể đều không có nước). Mỗi giờ máy thứ nhất, máy thứ hai, máy thứ ba bơm được lần lượt là 6m3, 10m3, 9m3. Thời gian bơm đầy bể của máy thứ hai ít hơn máy thứ nhấtlà 2 giờ. Tính thời gian của từng máy để bơm đầy bể.
Bài 4 (3,5đ) Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt cạnh BC tại I. Trên cạnh AC lấy điểm D sao cho AD = AB.
a) Chứng minh rằng BI = ID.
b) Tia DI cắt tia AB tại E. Chứng minh rằng ΔIBE=ΔIDCΔIBE=ΔIDC.
c) Chứng minh BD // EC.
d) Cho ∠ABC=2∠ACB.∠ABC=2∠ACB. Chứng minh rằng AB + BI = AC.
Bài 5 (1đ) a) Cho các số a, b, c, x, y, z thỏa mãn a + b + c = a2 + b2 + c2 = 1 và xa=yb=zcxa=yb=zc (các tỉ số đều có nghĩa). Chứng minh x2 + y2 + z2 = (x + y + z)2.
b) (Dành riêng cho lớp 7A)
Cho tam giác ABC có AB = 2 cm, BC = 4 cm và ˆABCABC^ = 600. Trên tia đối của tia BC lấy điểm D sao cho BD = BC, trên tia đối của tia BA lấy điểm E sao cho BE = BA. Tính diện tích tứ giác ACED.

Bài 1: a)√25–√494+√0,25=√52–√(72)2+√0,52=5–72+0,5=5–3,5+0,5=2.a)25–494+0,25=52–(72)2+0,52=5–72+0,5=5–3,5+0,5=2.
b)(–2527–3142)–(–727–342)=–2527–3142+727+342=(727–2527)+(342–3142)=–1827–2842=–23–23=–43b)(–2527–3142)–(–727–342)=–2527–3142+727+342=(727–2527)+(342–3142)=–1827–2842=–23–23=–43
c)10310–(9,5–0,25.18):0,5115–112=10310–(192–14.18):1265–32=10310–(192–92).26.25.2–3.55.2=10310–102.21210–1510=10310–10–310=10310–10010–310=310–310=–1c)10310–(9,5–0,25.18):0,5115–112=10310–(192–14.18):1265–32=10310–(192–92).26.25.2–3.55.2=10310–102.21210–1510=10310–10–310=10310–10010–310=310–310=–1
d)349.192–349.52–(120–14)2.(–12–19314)=349.(192–52)–(120–1.54.5)2.((–1).72.7–19314)=349.142–(120–520)2.(–714–19314)=37–(–420)2.(–20014)=37–(–15)2.(–1007)=37–125.(–100)7=37+47=77=1d)349.192–349.52–(120–14)2.(–12–19314)=349.(192–52)–(120–1.54.5)2.((–1).72.7–19314)=349.142–(120–520)2.(–714–19314)=37–(–420)2.(–20014)=37–(–15)2.(–1007)=37–125.(–100)7=37+47=77=1
Bài 2:
1) a) – Nếu 12x–16≥012x–16≥0 tứcx≥13x≥13thì∣∣∣12x–16∣∣∣=12x–16|12x–16|=12x–16
Ta có phương trình ⇔12x–16=13⇔12x–16=13
⇔12x=13+16⇔12x=13+16
⇔12x=12⇔12x=12
⇔x=1(tmdkx≥13)⇔x=1(tmdkx≥13)
– Nếu 12x–16<012x–16<0 tức là x <1313thì∣∣∣12x–16∣∣∣=–(12x–16)=16–12x|12x–16|=–(12x–16)=16–12x
Ta có phương trình ⇔16–12x=13⇔16–12x=13
⇔12x=16–13⇔12x=16–13
⇔12x=–16⇔12x=–16
⇔x=–13(tmdkx<13)⇔x=–13(tmdkx<13)
Vậy x = 1 hoặcx=–13.x=–13.
b) (4x2–3)3+8=0⇔(4x2–3)3=–8⇔4x2–3=–2⇔4x2=1⇔x2=14⇔|x|=12⇔⎡⎢ ⎢⎣x=12x=–12.(4x2–3)3+8=0⇔(4x2–3)3=–8⇔4x2–3=–2⇔4x2=1⇔x2=14⇔|x|=12⇔[x=12x=–12.
Vậyx=–12x=–12hoặcx=12x=12.
2) Vẽ đồ thị hàm sốy=–12xy=–12x .
– Khix=–2x=–2thìy=–12.(–2)=1y=–12.(–2)=1.
Vậy điểmC(–2;1)C(–2;1)thuộc đồ thị của hàm số .
Đồ thị của hàm số này là đường thẳng OC trong hình vẽ bên.
– Xét điểm A, B thấy điểm C thuộc đồ thị còn điểm B không thuộc đồ thị , thật vậy:
+ Khi x = –12–12thìy=–12.(–12)=6≠–6y=–12.(–12)=6≠–6nên điểm B(–12;–6–12;–6) không thuộc đồ thị .
+ Khix=2x=2thìy=–12.2=–1y=–12.2=–1nên điểmA(2;–1)A(2;–1)thuộc đồ thị .
Điểm A, C thuộc đồ thị còn điểm B không thuộc đồ thị nên 3 điểm A, B, C không thẳng hàng. (đpcm)
Bài 3: Gọi thời gian của từng máy để bơm đầy bể theo thứ tự làx,y,zx,y,z (giờ)(x,y,z>0).(x,y,z>0).
Vì thể tích 3 bể như nhau, nên thời gian của từng máy để bơm đầy b và thể tích nước bơm được mỗi giờ của mỗi máy là 2 đại lượng tỉ lệ nghịch.
Theo đề bài ta có: 6.x = 10.y = 9.z (1)
và x – y = 2 (2)
Từ (1) ta có: 6x90=10y90=9z906x90=10y90=9z90 (90 làBCNN(6; 10; 9)⇒x15=y9=z10⇒x15=y9=z10 (3)
Theo tính chất của dãy tỉ số bằng nhau, từ (3) và (2) ta có:x15=y9=z10=x–y15–9=26=13x15=y9=z10=x–y15–9=26=13
⇒x=153=5⇒x=153=5giờ, y=93=3y=93=3giờ vàz=103z=103giờ = 3 giờ 20 phút.
Vậy thời gian của từng máy để bơm đầy bể lần lượt là 5 giờ, 3 giờ và 3 giờ 20 phút.
Bài 4:
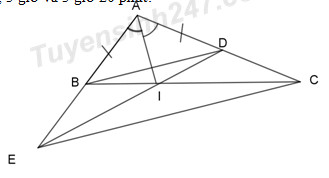
a) Xét tam giác ABI và tam giác ADI ta có:
∠BAI=∠DAI∠BAI=∠DAI (theo giả thiết)
AB=ADAB=AD (theo giả thiết)
AI: chung
⇒ΔABI=ΔADI(c–g–c)⇒ΔABI=ΔADI(c–g–c)
⇒BI=ID⇒BI=ID (2 cạnh tương ứng) (đpcm)
b) VìΔABI=ΔADI(c–g–c)ΔABI=ΔADI(c–g–c)nên:
∠ABI=∠ADI∠ABI=∠ADI (2 góc tương ứng) (1)
Mà: ∠ABE=∠ADC=1800∠ABE=∠ADC=1800 (2 góc bẹt) (2)
Từ (1) và (2) ta có: ∠ABE–∠ABI=∠ADC–∠ADI⇔∠IBE=∠IDC∠ABE–∠ABI=∠ADC–∠ADI⇔∠IBE=∠IDC
XétΔIBEΔIBEvàΔIDCΔIDC ta có:
∠IBE=∠IDC∠IBE=∠IDC (chứng minh trên)
∠BIE=∠DIC∠BIE=∠DIC (2 góc đối đỉnh)
BI=IDBI=ID (chứng minh trên)
⇒ΔIBE=ΔIDC(g–c–g)⇒ΔIBE=ΔIDC(g–c–g) (đpcm)
c) Ta có: BI = ID (chứng minh trên) ⇒ΔBID⇒ΔBIDcân tạiI⇒∠IBD=∠IDBI⇒∠IBD=∠IDB (tính chấtcủa tam giác cân) (1)
Ta lạicó: ΔIBE=ΔIDC(g–c–g)ΔIBE=ΔIDC(g–c–g) (chứng minh trên) ⇒IE=IC⇒IE=IC (2 cạnh tương ứng) ⇒ΔIEC⇒ΔIECcân tại I
⇒∠IEC=∠ICE⇒∠IEC=∠ICE (tính chấtcủa tam giác cân) (2)
Xét 2 tam giácΔIECΔIECvàΔIBDΔIBD ta có:
∠BID=∠EIC∠BID=∠EIC (2 góc đối đỉnh)
∠IBD+∠IDB+∠BID=∠IEC+∠ICE+∠EIC=1800∠IBD+∠IDB+∠BID=∠IEC+∠ICE+∠EIC=1800 (Tổng 3 góc của một tam giác bằng 1800) (3)
Từ (1), (2) và (3) ta có: 2∠IDB+∠BID=2∠IEC+∠EIC2∠IDB+∠BID=2∠IEC+∠EIC
⇒∠IDB=∠IEChay∠EDB=∠DEC⇒∠IDB=∠IEChay∠EDB=∠DEC (cặp góc so le trong bằng nhau)
⇒BD∥EC⇒BD∥EC (đpcm)
d)Ta cóΔIBE=ΔIDC(g–c–g)ΔIBE=ΔIDC(g–c–g)(chứng minh trên)
⇒∠BEI=∠DCI⇒∠BEI=∠DCI (2 góc tương ứng)
Lạicó: ∠BIE=∠DIC∠BIE=∠DIC (2 góc đối đỉnh)
⇒∠BEI+∠BIE=∠DCI+∠DIC⇒∠BEI+∠BIE=∠DCI+∠DIC (*)
Xét tam giác BIE ta có:
∠ABC=∠BIE+∠BEI∠ABC=∠BIE+∠BEI (gócngoàicủa 1 tam giác bằng tổng 2 góc trong không kề với nó) (**)
Từ (*) và (**) ta có: ∠ABC=∠DCI+∠DIC∠ABC=∠DCI+∠DIC hay ∠ABC=∠ACB+∠DIC∠ABC=∠ACB+∠DIC
Theo giảthiết, ta có: ∠ABC=2∠ACB∠ABC=2∠ACB
⇒∠DCI=∠DIC⇒ΔDIC⇒∠DCI=∠DIC⇒ΔDICcântạiD⇒DI=DCD⇒DI=DC.
Vì BI = ID (chứng minh trên) nên BI = DC.
⇒⇒ AC = AD + DC = AB + BI (đpcm)
Bài 5: a) Theo tính chất dãy tỉ số bằng nhau ta có:
xa=yb=zc=x+y+za+b+cxa=yb=zc=x+y+za+b+c=x+y+z1=x+y+z=x+y+z1=x+y+z (Theo giả thiết a + b + c = 1)
⇒(xa)2=(yb)2=(zc)2=(x+y+z)2⇒(xa)2=(yb)2=(zc)2=(x+y+z)2 (1)
Theo tính chất dãy tỉ số bằng nhau, ta lại có:
(xa)2=(yb)2=(zc)2(xa)2=(yb)2=(zc)2=x2+y2+z2a2+b2+c2=x2+y2+z21=x2+y2+z2=x2+y2+z2a2+b2+c2=x2+y2+z21=x2+y2+z2(Theo giả thiếta2+b2+c2=1a2+b2+c2=1) (2)
Từ (1) và (2) ta có: x2+y2+z2=(x+y+z)2(dpcm)x2+y2+z2=(x+y+z)2(dpcm)
b) XétΔABCΔABCvàΔEBDΔEBD ta có:
AB = EB (theo gt)
BD = BC (theo gt)
∠ABC=∠EBD∠ABC=∠EBD (cặp gócđối đỉnh bằng nhau)
⇒ΔABC=ΔEBD(c–g–c)⇒ΔABC=ΔEBD(c–g–c)
Chứng minh tươngtự ta có: ΔABD=ΔEBC(c–g–c)ΔABD=ΔEBC(c–g–c)
⇒SΔABC+SΔABD=SΔEBD+SΔEBC⇒SΔABC+SΔABD=SΔEBD+SΔEBC⇒SΔEDC=SΔACD=12SACED⇒SΔEDC=SΔACD=12SACED
Kẻ đường cao AH của tam giác ACD (H∈DCH∈DC)
Xét tam giác vuông AHB ta có:
∠BAH+∠ABH=900⇔∠BAH+600=900⇔∠BAH=300∠BAH+∠ABH=900⇔∠BAH+600=900⇔∠BAH=300
⇒BH=12AB=12.2=1cm⇒BH=12AB=12.2=1cm(Tam giác vuông có một góc bằng 30000000 thì cạnh đối diện góc đó bằng nửa cạnh huyền)
Áp dụng định lý Pitago vào tam giác vuông AHB, ta có:
AH2+BH2=AB2⇔AH2+12=22AH2+BH2=AB2⇔AH2+12=22
⇔AH2=4–1=3⇔AH=√3cm⇔AH2=4–1=3⇔AH=3cm
Vậy diện tích tứ giác ACED là: SACED=2.SΔACDSACED=2.SΔACD=2.12.AH.DC=AH.2BC=√3.2.4=8√3cm
đề Anh
I am a student. So I spend the day in a (1) _________ way. I get up from bed (2) _________ in the morning. First, I do my morning (3) _________ I wash my face and (4) _________ my teeth. I take great care of my teeth, because bad teeth are a sign of bad (5) _________. Then I take a little (6) _________ exercise. After taking exercise, I go out for a walk in the open (7) _________. There I breathe (8) _________ morning air. My mind and body are both (9) _________ . Then I return home. I say my short (10) _________.
II. Choose the word whose underlined part is pronounced differently.
Question 11.
A. come B. money
C. notebook D. Monday
Question 12.
A. couple B. though
C. soul D. elbow
Question 13.
A. seven B. vowel
C. very D. foot
III. Choose the odd one out.
Question 14.
A. friend B. parent
C. uncle D. aunt
Question 15.
A. small B. big
C. old D. meet
Question 16.
A. school B. classmate
C. theater D. market
IV. Choose A, B, C or D that best completes the sentences or substitutes for the underlined word or phrase.
Question 17. Do volunteers often spend time helping other people in ___________, orphanages or homes for the aged.
A. capitals B. markets
C. schools D. hospitals
Question 18. we are helping the poor people in the remote areas.
A. faraway B. nearby
C. small D. difficult
Question 19. During summer vacations, we teach children in ___________ areas how to read and write.
A. mountain B. urban
C. mountainous D. suburb
Question 20. What kind of ___________ work are you paripating in?
A. voluntarily B. volunteer
C. voluntary D. volunteerism
Question 21. People who are not in good health are ___________ people.
A. elderly B. homeless
C. rich D. sick
Question 22. I was absent ___________ class yesterday.
A. in B. of
C. from D. at
Question 23. He was delighted ___________ the present you gave him.
A. in B. to
C. for D. with
Question 24. It is very kind ___________ you to help them.
A. of B. in
C. about D. to
Question 25. It is difficult ___________ handicapped children to study with other children.
A. to B. for
C. on D. from
Question 26. I’m very grateful ___________ her for her help.
A. on B. of
C. about D. to
V. Read the text and choose the correct answer A, B, C, or D for each of the gaps.
EARTHWATCH
Have you ever wanted to do something different? Five years ago, Will Slade read about (27) ______ organization called Earthwatch. Earthwatch finds volunteers (28) ______ expeditons (29) ______ and explore different parts of the world.
Will decided (30) ______ an expedition to study elephants in Africa. “I wasn’t sure about it before I went.” say Will. “But in fact, I really enjoyed every minute of the expedition. We slept (31) ______ tents and we cooked our own food, but it was the great (32) ______ elephants and all the other animals there”. “I’ve (33) ______ all the expeditions, and I have seen some fantas places. How (34) ______ people have slept (35) ______ a beach, climbed a mountain, or see a whale? This world is such a beautiful place, but it’s disappearing fast. We have to learn more (36) ______ it if we are going to save it.”
Question 27.
A. a B. the
C. an D. some
Question 28.
A. to B. for
C. at D. on
Question 29.
A. studying B. studied
C. study D. to study
Question 30.
A. to join B. join
C. joining D. joined
Question 31.
A. on B. in
C. at D. under
Question 32.
A. see B. saw
C. seeing D. to see
Question 33.
A. enjoyed B. enjoy
C. enjoying D. to enjoy
Question 34.
A. much B. far
C. many D. long
Question 35.
A. in B. on
C. to D. above
Question 36.
A. at B. in
C. of D. about
VI. Choose the best sentence that can be made from the cues given.
Question 37. I / not / visited / museum / three months.
A. I haven’t visited the museum three months ago.
B. I havn’t visited the museum for three months.
C. I didn’t visited the museum for three months.
D. I haven’t visited the museum three months ago.
Question 38. Ms Linda / beautiful photos / few days ago.
A. Ms Linda took many beautiful photos a few days ago.
B. Ms Linda took much beautiful photos a few days ago.
C. Ms Linda took many beautiful photos few days ago.
D. Ms Linda took much beautiful photos few days ago.
Question 39. The students / arrived / because / traffic jam.
A. The students arrived late because the traffic jam.
B. The students arrived late because of the traffic jam.
C. The students arrived lately because the traffic jam.
D. The students arrived lately because of the traffic jam.
Question 40. I / eat / fruits / because / they / green.
A. I can’t eat these fruits because of they are green.
B. I can’t eat this fruits because of they are green.
C. I can’t eat these fruits because they are green.
D. I can’t eat this fruits because they are green.

Question 1. simple
Question 2. early
Question 3. duties
Question 4. brush
Question 5. health
Question 6. physical
Question 7. field
Question 8. pure
Question 9. refreshed
Question 10. prayer
| Question 11. C | Question 26. D |
| Question 12. A | Question 27. C |
| Question 13. D | Question 28. B |
| Question 14. A | Question 29. D |
| Question 15. D | Question 30. A |
| Question 16. B | Question 31. B |
| Question 17. D | Question 32. D |
| Question 18. A | Question 33. A |
| Question 19. C | Question 34. C |
| Question 20. C | Question 35. B |
| Question 21. D | Question 36. D |
| Question 22. C | Question 37. B |
| Question 23. D | Question 38. A |
| Question 24. A | Question 39. B |
| Question 25. B | Question 40. C |

Bài 1: Thực hiện phép tính:

Bài 2: Tìm x, biết:

Bài 3:
Ba đội máy cày có 18 máy (có cùng năng suất) làm việc trên 3 cánh đồng có cùng diện tích. Đội 1 làm xong trong 3 ngày, đội 2 trong 4 ngày và đội 3 trong 6 ngày. Hỏi mỗi đội có mấy máy?
Bài 4: Cho ABC có AB = AC, M là trung điểm của BC.
a. Chứng minh: ABM = ACM.
b. Trên tia đối của MA lấy D sao cho MD = MA. Chứng minh: AC = BD.
c. Chứng minh: AB // CD.
d. Trên nửa mặt phẳng bờ là AC không chứa B, vẽ tia Ax // BC, lấy IAx sao cho AI = BC. Chứng minh: D, C, I thẳng hàng.

ddaaaaaaaaay đầu bài sai !!!
và tớ cũng trà lời lần thứ 2 rồi đấy !!!!

Giả sử \(x=\frac{a}{m},y=\frac{b}{m}(a,b,m\inℤ,m\ge0)\)
Vì x < y nên ta suy ra a < b
Ta có : \(x=\frac{a}{m},y=\frac{b}{m}\Leftrightarrow x=\frac{2a}{2m},y=\frac{2b}{2m}\)
Mà a < b nên a + a < a + b <=> 2a < a + b
Do 2a < a + b thì x < y [1]
Lại có : a < b nên a + b < b + b <=> a + b < 2b
Mà a + b < 2b <=> x < z [2]
Từ 1 và 2 suy ra x < z < y \((đpcm)\)


Bấy giờ Trần Cảnh còn nhỏ mới 11 tuổi, vợ là Lý Chiêu Hoàng, vị vua cuối cùng của dòng họ Lý. Vì nhường ngôi cho chồng nên trăm họ và tôn thất nhà Lý dị nghị nhà Trần cướp ngôi. Trần Thủ Độ rất lo lắng.
Bấy giờ Trần Liễu, anh ruột vua Trần Cảnh lấy công chúa Thuận Thiên, chị gái Chiêu Hoàng đang có mang. Trần Thủ Độ ép Liễu nhường vợ cho Cảnh để chắc có một đứa con cho Cảnh. Liễu nổi loạn. Thủ Độ dẹp tan nhưng tha chết cho Liễu. Song điều này không dẹp nổi lòng thù hận của Liễu. Vì thế Liễu kén thày dạy giỏi cho con trai mình thành bậc văn võ toàn tài, ký thác cho con mối thù sâu nặng. Người con trai ấy chính là Trần Quốc Tuấn.
Bấy giờ quân Nguyên sang xâm chiếm Việt Nam. Trần Quốc Tuấn đã giao hảo hoà hiếu với Trần Quang Khải. Hai người là hai đầu mối của hai chi trong họ Trần đồng thời một người là con Trần Liễu, một người là con Trần Cảnh, hai anh em đối đầu của thế hệ trước. Sự hoà hợp của hai người chính là sự thống nhất ý chí của toàn bộ vương triều Trần, đảm bảo đánh thắng quân Nguyên hung hãn.
Chuyện kể rằng: Thời ấy tại bến Đông, ông chủ động mời Thái sư Trần Quang Khải sang thuyền mình trò chuyện, chơi cờ và sai nấu nước thơm tự mình tắm rửa cho Quang Khải...
Rồi một lần khác, ông đem việc xích mích trong dòng họ dò ý các con. Trần Quốc Tảng có ý khích ông cướp ngôi vua của chi thứ, ông nổi giận định rút gươm toan chém chết Quốc Tảng. Do các con và những người tâm phúc xúm vào van xin, ông bớt giận, dừng gươm và bảo rằng: Từ nay cho đến khi ta nhắm mắt, ta sẽ không nhìn mặt thằng nghịch tử, phản thầy này nữa!
Trong chiến tranh, ông luôn hộ giá bên vua, tay chỉ cầm cây gậy bịt sắt. Thế mà vẫn có lời dị nghị, sợ ông sát vua. Ông bèn bỏ luôn phần gậy bịt sắt chỉ chống gậy không mỗi khi gần cận nhà vua. Và sự nghi kỵ cũng chấm dứt. Giỏi tâm lý, chú ý từng việc nhỏ để tránh hiềm nghi, yên lòng quan, yên lòng dân, đoàn kết mọi người vì nghĩa lớn dân tộc. Ông là một tấm lòng trung trinh son sắt vì vua vì nước.
Năm 1283, Vua giao quyền tiết chế cho Trần Quốc Tuấn. Ông biết dùng người tài như các anh hùng: Phạm Ngũ Lão, Dã Tượng, Yết Kiêu, Trương Hán Siêu... đều từ cửa tướng của ông mà ra. Ông rất thương binh lính, họ cũng rất tin yêu ông. Đội quân cha con ấy trở thành đội quân bách thắng.
Bản Hịch tướng sĩ viết bằng giọng văn thống thiết hùng hồn mang tầm tư tưởng của một bậc đại bút .
Trần Quốc Tuấn là một bậc tướng tài có đủ tài đức. Là tướng nhân, ông thương dân, thương quân, chỉ cho quân dân con đường sáng. Là tướng nghĩa, ông coi việc phải hơn điều lợi. Là tướng chí, ông biết lẽ đời sẽ dẫn đến đâu. Là tướng dũng, ông sẵn sàng xông pha nơi nguy hiểm để đánh giặc, lập công, cho nên trận Bạch Đằng oanh liệt nghìn đời là đại công của ông. Là tướng tín, ông bày tỏ trước cho quân lính biết theo ông thì sẽ được gì, trái lời ông thì sẽ bị gì. Cho nên cả ba lần đánh giặc Nguyên - Mông , Trần Quốc Tuấn đều lập công lớn.
Mùa thu tháng Tám, ngày 20 năm Canh Tí, Hưng Long thứ 8 (1300) "Bình Bắc Đại nguyên soái" Hưng Đạo đại vương qua đời.
Theo lời dặn lại, thi hài ông được hoả táng thu vào bình đồng và chôn trong vườn An Lạc, giữa cánh rừng An Sinh miền Đông Bắc, không xây lăng mộ, san phẳng trồng cây như cũ.
Khi ông mất, vua phong cho ông tước Hưng Đạo đại vương. Triều đình lập đền thờ ông tại Vạn Kiếp, Chí Linh, ấp phong của ông thuở sinh thời. Công lao sự nghiệp của ông khó kể hết. Vua coi như bậc trượng phu, trăm họ kính trọng ông gọi là Hưng Đạo Đại vương. Trần Hưng Đạo là một anh hùng dân tộc, một danh nhân văn hoá Việt Nam.
Nguồn: http://www.btlsqsvn.org.vn/Chi_tiet_danh_nhan/?%5E?=37
Trần Quốc Tuấn là con trai của An Sinh vương Trần Liễu, cháu gọi vua Trần Thái Tông bằng chú ruột. Nguyên quán:xã Tiến Đức, Hưng Hà, Thái Bình. Là người văn võ song toàn. Trần Quốc Tuấn trở thành võ quan nhà Trần khi còn rất trẻ.Tháng 9 (âm lịch) năm Đinh Tỵ (1257), ông giữ quyền “tiết chế” để chuẩn bị chống lại cuộc xâm lược của quân Mông-Nguyên lần 1. Dưới sự lãnh đạo của Trần Quốc Tuấn, quân đội nhà Trần đã vượt qua vô vàn khó khăn và hiểm nguy, ba lần đánh giặc Mông-Nguyên xâm lược giành thắng lợi lẫy lừng. Công lao to lớn này đã đưa ông lên hàng “thiên tài quân sự có tầm chiến lược, và là một anh hùng dân tộc bậc nhất của nhà Trần”.Tháng 4-1289 Ông được phong tước Hưng Đạo Đại Vương.Tháng 6 (âm lịch) năm Canh...