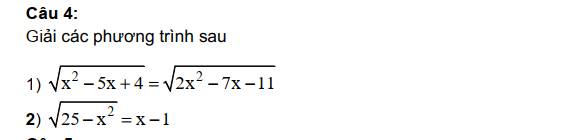Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

12 sai, C mới là đáp án đúng
13 sai, A đúng, \(sin-sin=2cos...sin...\)
18.
\(\Leftrightarrow\left\{{}\begin{matrix}a=m>0\\\Delta'=m^2-m\left(-m+3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m^2-3m< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow m=1\)
Đáp án B
22.
Để pt có 2 nghiệm pb \(\Leftrightarrow\left\{{}\begin{matrix}m-2\ne0\\\Delta'=\left(2m-3\right)^2-\left(m-2\right)\left(5m-6\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\-m^2+4m-3>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\1< m< 3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2\left(2m-3\right)}{m-2}\\x_1x_2=\dfrac{5m-6}{m-2}\end{matrix}\right.\)
\(\dfrac{-2\left(2m-3\right)}{m-2}+\dfrac{5m-6}{m-2}\le0\)
\(\Leftrightarrow\dfrac{m}{m-2}\le0\) \(\Leftrightarrow0\le m< 2\)
Kết hợp điều kiện delta \(\Rightarrow1< m< 2\)
24.
Đề bài câu này dính lỗi, ko có điểm M nào cả, chắc là đường thẳng đi qua A
Đường tròn (C) tâm I(1;-2) bán kính R=4
\(\overrightarrow{IA}=\left(1;3\right)\)
Gọi d là đường thẳng qua A và cắt (C) tại 2 điểm B và C. Gọi H là trung điểm BC
\(\Rightarrow IH\perp BC\Rightarrow IH=d\left(I;d\right)\)
Theo định lý đường xiên - đường vuông góc ta luôn có: \(IH\le IA\)
Áp dụng Pitago cho tam giác vuông IBH:
\(BH=\sqrt{IB^2-IH^2}\Leftrightarrow\dfrac{BC}{2}=\sqrt{16-IH^2}\)
\(\Rightarrow BC_{min}\) khi \(IH_{max}\Leftrightarrow IH=IA\)
\(\Leftrightarrow IA\perp d\Rightarrow d\) nhận \(\overrightarrow{IA}\) là 1 vtpt
Phương trình d:
\(1\left(x-2\right)+3\left(y-1\right)=0\Leftrightarrow x+3y-5=0\)

11c.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}\dfrac{16a-b^2}{4a}=\dfrac{9}{2}\\16a+4b+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2b^2=-4a\\b=-4a-1\end{matrix}\right.\)
\(\Rightarrow2b^2-b=1\Leftrightarrow2b^2-b-1=0\Rightarrow\left[{}\begin{matrix}b=1\Rightarrow a=-\dfrac{1}{2}\\b=-\dfrac{1}{2}\Rightarrow a=-\dfrac{1}{8}\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=-\dfrac{1}{2}x^2+x+4\\y=-\dfrac{1}{8}x^2-\dfrac{1}{2}x+4\end{matrix}\right.\)
4f.
Từ đề bài ta có:
\(\left\{{}\begin{matrix}1+b+c=0\\\dfrac{4c-b^2}{4}=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=-b-1\\c=\dfrac{b^2}{4}-1\end{matrix}\right.\)
\(\Rightarrow\dfrac{b^2}{4}+b=0\)
\(\Rightarrow\left[{}\begin{matrix}b=0\Rightarrow c=-1\\b=-4\Rightarrow c=3\end{matrix}\right.\)
Có 2 parabol thỏa mãn: \(\left[{}\begin{matrix}y=x^2-1\\y=x^2-4x+3\end{matrix}\right.\)

1: =>2x^2-7x-11=x^2-5x+4
=>x^2-2x-15=0
=>(x-5)(x+3)=0
=>x=5 hoặc x=-3
2: =>x>=1 và 25-x^2=x^2-2x+1
=>x^2-2x+1-25+x^2=0 và x>=1
=>2x^2-2x-24=0 và x>=1
=>x=4
1.
Bình phương hai vế pt đã cho ta được:
\(x^2-5x+4=2x^2-7x-11\)
\(\Rightarrow x^2-2x-15=0\)
\(\Rightarrow x=5\) hoặc \(x=-3\)
Thay lần lượt hai giá trị trên vào pt đã cho ta thấy đều thỏa mãn
Vậy nghiệm của pt là \(S=\left\{-3;5\right\}\)
2.
Bình phương 2 vế pt đã cho:
\(25-x^2=\left(x-1\right)^2\)
\(\Rightarrow25-x^2=x^2-2x-1\)
\(\Rightarrow2x^2-2x-24=0\)
\(\Rightarrow x=4\) hoặc \(x=-3\)
Lần lượt thay các giá trị trên vào pt đã cho ta thấy chỉ có \(x=4\) thỏa mãn
Vậy nghiệm của pt đã cho là \(S=\left\{4\right\}\)

1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t