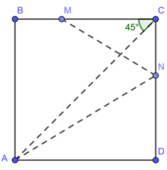
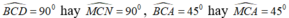Giả sử hình vuông ABCD thỏa mãn đề bài đã dựng được. Qua M dựng đường thẳng vuông góc với AM cắt AB ở P, cắt CD ở Q, ta có :△MBP = △MCQ (g.c.g), suy ra MP = MQ.Mặt khác ta còn chứng minh được PQ = AM.Từ đó xác định được hai điểm P, Q rồi suy ra điểm B, điểm C, điểm D để được hình vuông ABCD.
Giả sử hình vuông ABCD thỏa mãn đề bài đã dựng được. Qua M dựng đường thẳng vuông góc với AM cắt AB ở P, cắt CD ở Q, ta có :△MBP = △MCQ (g.c.g), suy ra MP = MQ.Mặt khác ta còn chứng minh được PQ = AM.Từ đó xác định được hai điểm P, Q rồi suy ra điểm B, điểm C, điểm D để được hình vuông ABCD.