PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
30 tháng 11 2023
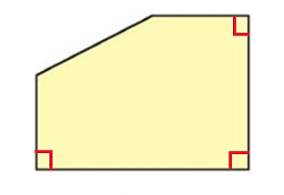
a) Gấp hình theo yêu cầu bài toán sau đó kiểm tra em thấy các góc vừa gấp được là các góc vuông.
b) Trong hình bên có 3 góc vuông. Đó là các góc như hình vẽ sau:
HQ
Hà Quang Minh
Giáo viên
30 tháng 11 2023
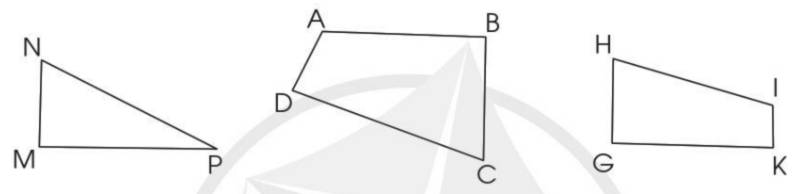
a) Tam giác ABC có:
- Ba đỉnh: A, B, C
- Ba cạnh: AB, AC, BC
- Ba góc: A, B, C
Tứ giác MNPQ có:
- Các đỉnh: M, N, P, Q.
- Các cạnh: MN, NP, PQ, QM.
- Các góc: M, N, P, Q
Tứ giác GHIK có:
- Các đỉnh: G, H, I, K.
- Các cạnh: GH, HI, IK, KG.
- Các góc: G, H, I, K
b) Tam giác ABC có 1 góc vuông.
Tứ giác MNPQ có 2 góc vuông.
Tứ giác GHIK có 1 góc vuông.
28 tháng 3 2023
`a,`
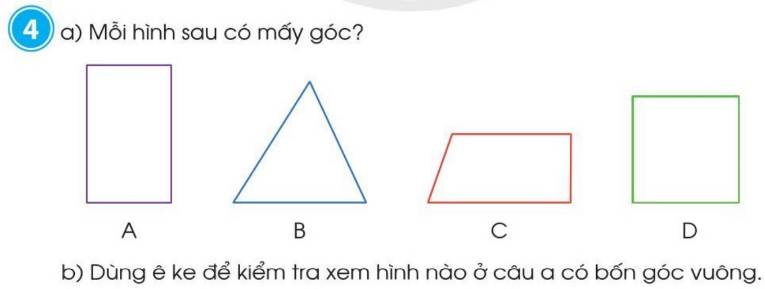
Hình `A:` có `4` góc
Hình `B:` có `3` góc
Hình `C:` có `4` góc
Hình `D:` có `4` góc
`b,` Hình `A, D` có `4` góc vuông
PT
1
NT
1
28 tháng 3 2023
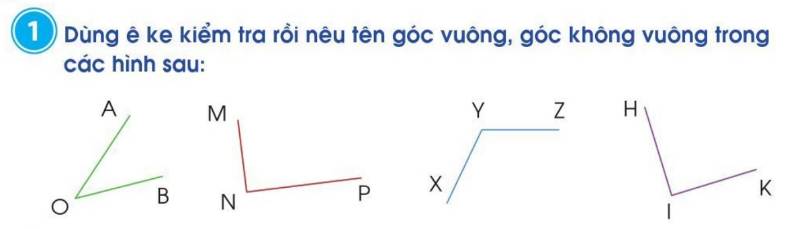
`-` Hình `MNP:`
Góc vuông: `N`
góc không vuông: `M, P`
`-` Hình `HIK:`
Góc vuông: `I`
góc không vuông: `H, K`
CM
19 tháng 12 2018
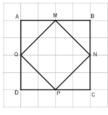
a) (Học sinh tự vẽ)
b) Các góc vuông đó là:
Góc đỉnh A; cạnh AM, AQ.
Góc đỉnh B; cạnh BM, BN.
Góc đỉnh C; cạnh CP, CN.
Góc đỉnh D; cạnh DP, DQ.
Góc đỉnh M; cạnh MQ, MN.
Góc đỉnh N; cạnh NM, NP.
Góc đỉnh P; cạnh PN, PQ.
Góc đỉnh Q; cạnh QP, QM.
HQ
Hà Quang Minh
Giáo viên
30 tháng 11 2023
Em sử dụng ê ke và kiểm tra được hai bán kính OC và OB tạo thành 1 góc vuông vì điểm O trùng với đỉnh của ê ke, hai cạnh OC và OB trùng với 2 cạnh của ê ke.
HQ
Hà Quang Minh
Giáo viên
29 tháng 11 2023
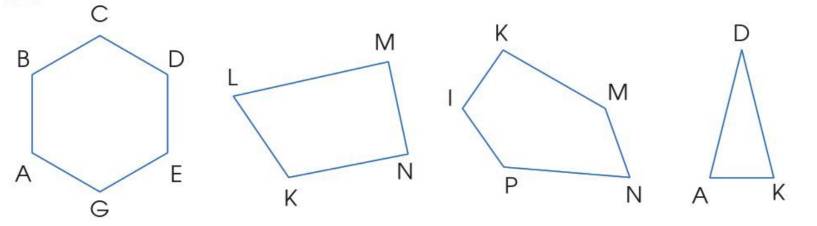
a) Tam giác ADK, tứ giác KLMN.
b) Dùng ê ke để kiểm tra các hình trên, ta thấy:
- Hình tứ giác KLMN có góc vuông:
+ Góc vuông đỉnh M
+ Góc vuông đỉnh N
HQ
Hà Quang Minh
Giáo viên
29 tháng 11 2023
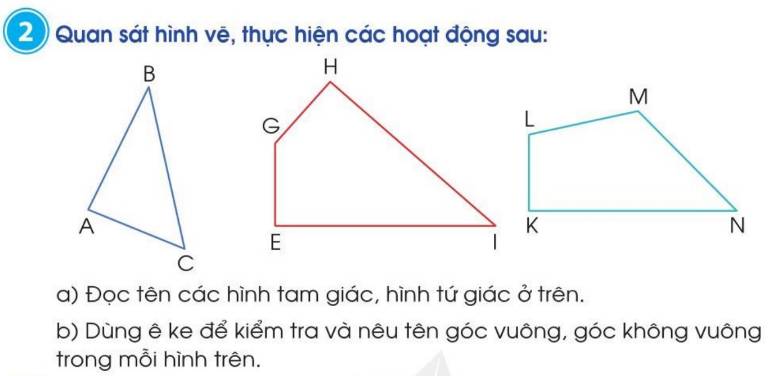
a) Hình tam giác ABC, hình tứ giác EGHI, hình tứ giác KLMN.
b)
Hình tam giác ABC có góc vuông đỉnh A, cạnh AB và AC.
Hình tứ giác GHIE có góc vuông đỉnh E, cạnh EG và EI; góc vuông đỉnh H, cạnh HG và HI.
Hình tứ giác KLMN có góc vuông đỉnh K cạnh KL và KN.
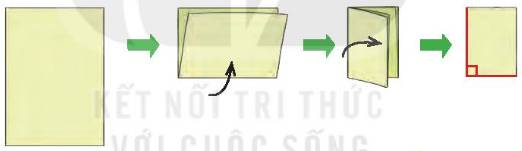
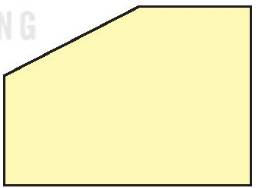
Đáp án:
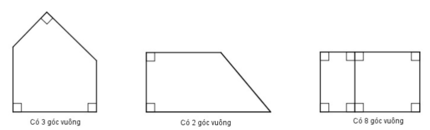
Có 2 góc vuông