Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo a) ΔEKI = ΔGKJ nên KI = KJ.
Mặt khác, theo giả thiết K là trung điểm của AL nên KA = KL.
Suy ra: KA – KI = KL – KJ hay IA= JL.
Ta có: ∆ACH= ∆ GAJ ( theo a) nên HC = AJ;
∆ABH = ∆ EAI nên BH = AI.
+) Suy ra:
AL = AJ + JL = AJ + AI = HC + HB = BC

Nói chính xác luôn là tam giác vuông cân, lại bày hình vuông chi

a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔAGE và ΔCDE có
EA=EC
\(\widehat{AEG}=\widehat{CED}\)
EG=ED
Do đó: ΔAGE=ΔCDE

a: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
góc HAM=góc KAM
=>ΔAHM=ΔAKM
=>AK=AH
góc BAM+góc CAM=90 độ
góc BMA+góc MAH=90 độ
mà góc CAM=góc HAM
nên góc BAM=góc BMA
=>ΔBAM cân tại B
b: Xét ΔAIC có
CH,IK là đường cao
CH cắt IK tại M
=>M là trực tâm
=>AM vuông góc CI
Xét ΔACI có
AM vừa là đường cao, vừa là phân giác
=>ΔACI cân tại A
Xét ΔAIC có AH/AI=AK/AC
nên KH//IC
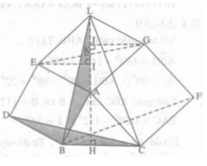
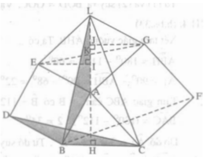
+) Xét tam giác EIA vuông tại I nên :
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.