Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm

Đối với hàm số y = 2x2, khi x ≠ 0 giá trị của y luôn dương
Khi x = 0 thì giá trị của y =0
Đối với hàm số y = - 2x2, khi x ≠ 0 giá trị của y luôn âm
Khi x = 0 thì giá trị của y =0

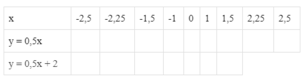
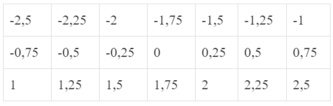
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
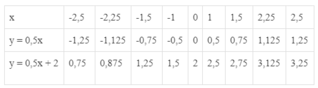
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.

| x | -2,5 | -2,25 | -2 | -1,75 | -1,5 | -1,25 | -1 |
| y = f(x) = 1,2x | -3 | -2,7 | -2,4 | -2,1 | -1,8 | -1,5 | -1,2 |
| x | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 |
| y = f(x) = 1,2x | -0,9 | -0,6 | -0,3 | 0 | 0,3 | 0,6 | 0,9 |
| x | 1 | 1,25 | 1,5 | 1,75 | 2 | 2,25 | 2,5 |
| y = f(x) = 1,2x | 1,2 | 1,5 | 1,8 | 2,1 | 2,4 | 2,7 | 3 |

Bài 1:
Hàm số y=(m-3)x+4 đồng biến trên R khi m-3>0
=>m>3
Hàm số y=(m-3)x+4 nghịch biến trên R khi m-3<0
=>m<3
Bài 4:
a: Vì \(a=3-\sqrt{2}>0\)
nên hàm số \(y=\left(3-\sqrt{2}\right)x+1\) đồng biến trên R
b: Khi x=0 thì \(y=0\left(3-\sqrt{2}\right)+1=1\)
Khi x=1 thì \(y=\left(3-\sqrt{2}\right)\cdot1+1=3-\sqrt{2}+1=4-\sqrt{2}\)
Khi \(x=\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\cdot\sqrt{2}+1=3\sqrt{2}-2+1=3\sqrt{2}-1\)
Khi \(x=3+\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)\left(3+\sqrt{2}\right)-1\)
=9-4-1
=9-5
=4
Khi \(x=3-\sqrt{2}\) thì \(y=\left(3-\sqrt{2}\right)^2-1\)
\(=11-6\sqrt{2}-1=10-6\sqrt{2}\)

Ta có:
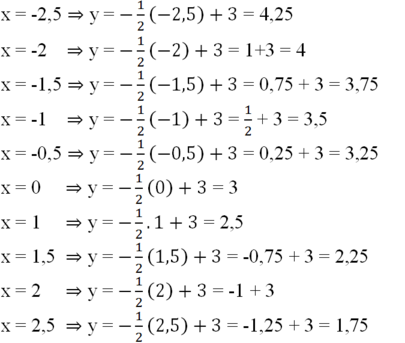
Ta được bảng sau:

b) Hàm số đã cho là hàm số nghịch biến trên R vì khi giá trị của biến x tăng lên mà giá trị tương ứng f(x) lại giảm đi.

Vẽ hình:
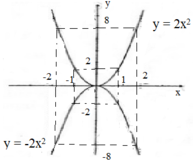
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

Hàm số y = f(x) = a x 2 , a ≠ 0
Vì hai giá trị đối nhau của x là x và –x thì x 2 = - x 2
⇒ f(x) = f(-x)
Vậy hai giá trị đối nhau của x thì giá trị tương ứng của hàm số bằng nhau.

Vẽ hình:
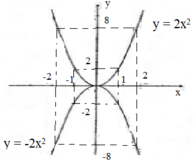
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

* Hàm số y = 2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y giảm
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y tăng
* Hàm số y = -2x2
- Khi x tăng nhưng luôn luôn âm thì giá trị tương ứng của y tăng
- Khi x tăng nhưng luôn luôn dương thì giá trị tương ứng của y giảm