Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Phương pháp:
Ba số a, b, c lập thành cấp số ciingj khi và chỉ khi a + c = 2b
Cách giải:


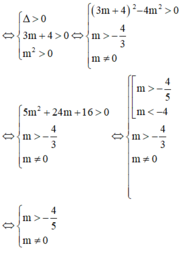


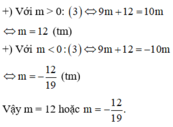

Hoành độ giao điểm của (C) và Ox là nghiệm phương trình
x - 1 x 2 - 3 m - 1 x + 1 = 0 ⇔ x = 1 g x = x 2 - 3 m - 1 x + 1 = 0 1
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt thì (1) có 2 nghiệm phân biệt khác 1.
Khi đó ∆ > 0 g 1 ≠ 0
⇔ m > 1 m < - 1 3 m ≠ 1 ⇔ m > 1 m < - 1 3
Giả sử x 3 = 1
Theo đề thì phương trình (1) có hai nghiệm x 1 ; x 2
x 1 2 + x 2 2 > 14 ⇔ x 1 + x 2 2 - 2 x 1 x 2 > 14 ⇔ m > 5 3 m < - 1
(thỏa mãn)
Vậy m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
Đáp án C

Đáp án B
y = 0 ⇔ x 2 = 1 x 2 = 2 m + 1 . có 4 nghiệm phân biệt khi
2 m + 1 > 0 ; 2 m + 1 ≠ 1 ⇔ m > − 1 ; m ≠ 0 .
Khi đó 4 nghiệm là − 2 m + 1 ; − 1 ; 1 ; 2 m + 1
4 nghiệm lập thành cấp số cộng có trường hợp sau sắp xếp theo thứ tự sau
TH1: − 1 ; − 2 m + 1 ; 2 m + 1 ; 1 ⇒ khoảng cách giữa chúng là bằng nhau ⇔ 1 − 2 m + 1 = 2 2 m + 1 ⇔ 3 2 m + 1 = 1 ⇔ m = − 4 9 .
TH2: − 2 m + 1 ; − 1 ; 1 ; 2 m + 1 ⇒ khoảng cách giữa chung là bằng nhau
⇔ 2 m + 1 − 1 = 2 ⇔ m = 4










Chọn A.
Gọi x 1 ; x 2 ; x 3 là 3 nghiệm phân biệt của PT x 3 − 3 m x 2 + 9 x − 7 = 0
Áp dụng định lý Vi – ét cho PT bậc 3 có:
x 1 + x 2 + x 3 = − b a x 1 x 2 + x 1 x 3 + x 2 x 3 = c a x 1 x 2 x 3 = − d a nên có x 1 + x 2 + x 3 = − − 3 m 1 = 3 m x 1 x 2 + x 1 x 3 + x 2 x 3 = 9 1 = 9 x 1 x 2 x 3 = − 7 1 = 7
Để x 1 ; x 2 ; x 3 lập thành 1 cấp số cộng, ta giả sử u 1 = x 1 , u 2 = x 2 ; u 3 = x 3 tức là x 2 = x 1 + d , x 3 = x 1 = 2 d
Khi đó ta có:
3 x 1 + 3 d = 3 m x 1 x 1 + d + x 1 x 1 + 2 d + x 1 + d x 1 + 2 d = 9 x 1 x 1 + d x 1 + 2 d = 7
⇔ x 1 = m − d m − d m − d + d + m − d m − d + 2 d + m − d + d m − d + 2 d = 9 m − d m − d + d m − d + 2 d = 7
⇔ x 1 = m − d m − d m + m − d m + d + m m + d = 9 m − d m m + d = 7
⇔ x 1 = m − d m 2 − m d + m 2 + m d + m 2 − d 2 = 9 m − d m m + d = 7
⇔ x 1 = m − d 3 m 2 − d 2 = 9 m − d m m + d = 7 ⇔ x 1 = m − d d 2 = 3 m 2 − 9 m m 2 − d 2 = 7
⇔ x 1 = m − d d 2 = 3 m 2 − 9 m m 2 − 3 m 2 − 9 = 7 ⇔ x 1 = m − d d 2 = 3 m 2 − 9 m − 2 m 2 + 9 = 7
⇔ x 1 = m − d d 2 = 3 m 2 + 9 − 2 m 3 + 9 m = 7 ⇔ m = 1 m = − 1 + 15 2 m = − 1 − 15 2