Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

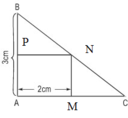
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
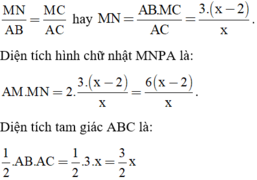
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
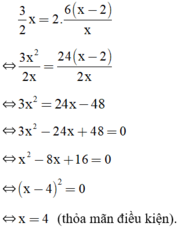
Vậy độ dài đoạn thẳng AC là 4cm.

3\(a^2\)+4a+1=3\(a^2\)+3a+a+1
=(3\(a^2\)+3a)+(a+1)
=3a(a+1)+(a+1)
=(a+1)(3a+1)

Mình vẽ hơi xấu nên nó k bằng nhau ^_^
a) ta thấy chiều dài của hcn B là cạnh của đáy S
Cạnh đầu tiên của đáy là 20 - 2x
Ta thấy chiều dài của hcn A là cạnh của đáy S
Cạnh thứ hai của đáy là 20 - 2x
Vậy Diện tích đáy S là (20 - 2x)2
b) khi gấp lại thành hình hộp chữ nhật thì x cũng là chiều cao của hình nên
Thể tích HHCN là x(20 - 2x)2

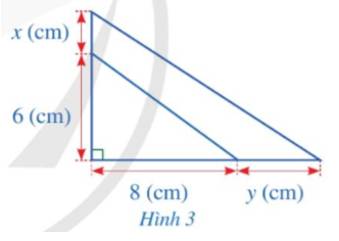
a) Đa thức biểu thị diện tích phần tăng thêm của miếng bìa là:
\(\dfrac{1}{2}\cdot\left(6+x\right)\cdot\left(8+y\right)-\dfrac{1}{2}\cdot6\cdot8\)
\(=\dfrac{1}{2}\cdot\left(48+6y+8x+xy\right)-3\cdot8\)
\(=24+3y+4x+\dfrac{xy}{2}-24\)
\(=3y+4x+\dfrac{xy}{2}\)
b) Phần diện tích tăng thêm là:
\(3\cdot4+4\cdot2+\dfrac{2\cdot4}{2}=24\left(cm^2\right)\)
a) Diện tích tam giác sau khi tăng thêm:
(6 + x).(8 + y) : 2
= (48 + 6y + 8x + xy) : 2
= 24 + 3y + 4x + xy/2
Diện tích phần tăng thêm:
24 + 3y + 4x + xy/2 - 6.8:2
= 4x + 3y + xy/2 (cm)²
b) Khi x = 2 và y = 4 thì diện tích phần tăng thêm là:
4.2 + 3.4 + 2.4/2
= 8 + 12 + 4
= 24 (cm²)

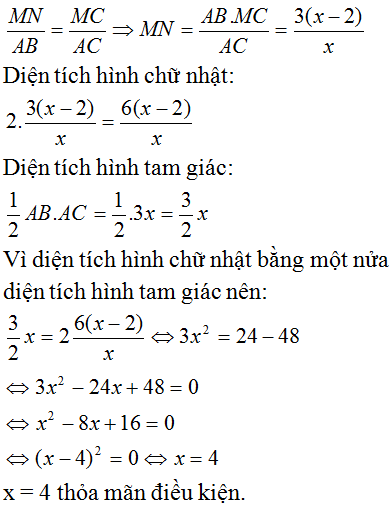
Đáp án B
Gọi x (cm) là độ dài cạnh AC (x > 2).
Gọi hình chữ nhật là MNPA như hình vẽ.
Ta có: MC = AC – AM = x – 2 (cm)
Vì MN // AB nên theo định lý Talet ta có tỉ lệ:
Vì diện tích tam giác ABC gấp đôi diện tích hình chữ nhật MNPA nên ta có phương trình:
Vậy độ dài đoạn thẳng AC là 4cm.