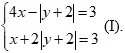Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

115.
+) 312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
116.
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
120.
5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
122.
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
Bài 115
312312 là một hợp số
Ta thấy 312 là 1 số chẵn nên 312 ít nhất là chia hết cho số 2, tưc là 312 có ước là 2 khác với 1 và 312. Nên 312 là một hợp số.
+) 213213 là một hợp số.
giải thích: tổng các chữ số của 213213 là 2+1+3=62+1+3=6 chia hết cho 33 nên 213213 ⋮⋮ 33, nghĩa là 213213 có ước là 33, khác 11 và 213213 do đó nó là hợp số .
+) 435435 là một hợp số
giải thích: 435435 có chữ số tận cùng là 55 nên 435435 ⋮⋮ 55 nghĩa là 435435 có ước là 55 khác 11 và 435435 do đó nó là hợp số.
+) 417417 là một hợp số.
giải thích: 417417 có tổng các chữ số là 4+1+7=124+1+7=12 chia hết cho 33 nên 417417 ⋮⋮ 33, nghĩa là 417417 có ước là 33, khác 11 và 417417 do đó nó là hợp số.
+) 33113311 là một hợp số.
giải thích: 3311=11.3013311=11.301 nên 33113311 có ước là 1111 và 301301. Vậy 33113311 là một hợp số.
+) 6767 là một số nguyên tố vì nó chỉ có hai ước là 11 và 6767.
Bài 116
83∈P83∈P, (vì 8383 chỉ có hai ước là 11 và chính nó)
9191 ∉∉ PP, (vì 9191 có các ước 1,7,13,911,7,13,91 do đó nó không phải số nguyên tố)
15∈N15∈N,
P⊂NP⊂N. (dựa vào định nghĩa số nguyên tố là số tự nhiên chỉ có hai ước là 11 và chính nó).
Bài 120
¯¯¯¯¯¯5∗5∗¯
∗∈{0,1,2,3,4,5,6,7,8,9}∗∈{0,1,2,3,4,5,6,7,8,9}
Do đó ta xét ∗∗ với từng giá trị
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯5∗5∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 5555 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 5151 có tổng các chữ số là 5+1=65+1=6 chia hết cho 33 do đó 5151 chia hết cho 33, trường hợp này loại
+) Nếu ∗=3∗=3 thì 5353 là số nguyên tố
+) Nếu ∗=7∗=7 thì 5757 có tổng các chữ số là 5+7=125+7=12 chia hết cho 33 do đó 5757 chia hết cho 33, trường hợp này loại.
+) Nếu ∗=9∗=9 thì 5959 là số nguyên tố.
Vậy * = {3; 9}
¯¯¯¯¯¯9∗9∗¯
Tương tự ta xét như trên và tìm được số 9797 là số nguyên tố.
+) Nếu ∗∈{0,2,4,6,8}∗∈{0,2,4,6,8} thì ¯¯¯¯¯¯9∗9∗¯ chia hết cho 22 do đó các trương hợp này không thỏa mãn.
+) Nếu ∗=5∗=5 thì 9595 chia hết cho 55 nên trường hợp này không thỏa mãn.
+) Nếu ∗=1∗=1 thì 9191 chia hết cho 77 do đó trường hợp này loại.
+) Nếu ∗=3∗=3 thì 9393 có tổng các chữ số là 9+3=129+3=12 nên chia hết cho 3 do đó 9393 là hợp số, do đó trường hợp này loại.
+) Nếu ∗=7∗=7 thì 9797 là một số nguyên tố.
+) Nếu ∗=9∗=9 thì 9999 là một hợp số vì cỏ tổng các chữ số là: 9+9=189+9=18 chia hết cho 33 và 99. Do đó trường hợp này loại.
Vậy * = 7
Bài 122
a) Đúng, vì có 22 và 33 là hai số tự nhiên liên tiếp đều là số nguyên tố;
b) Đúng, đó là 3,5,73,5,7;
c) Sai, vì 22 là số chẵn đồng thời cũng là số nguyên tố;
d) Sai vì 22 cũng là số nguyên tố.
k cho mk nha

125;
a;60 |2
30 |2
15 |3
5 |5
1
Do đó 60=2^2*3*5
b;84|2
42|2
21|3
7|7
1
Do đó 84=2^2*3*5
c; 285|3
95|5
19|19
1
Do đó 285=3*5*19
d; 1035|3
345|3
115|5
23|23
1
Do đó 1035=3^2*5*23
e; 400|2
200|2
100|2
50|2
25|5
5|5
1
Do đó 400=24*5^2
câu G bạn tự làm nha

Bài 125)
a)
![]()
Vậy: 60=22.3.560=22.3.5;
b)
![]()
Vậy: 84=22.3.784=22.3.7;
c)
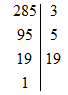
Vậy: 285=3.5.19285=3.5.19;
d)
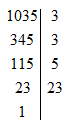
Vậy: 1035=32.5.231035=32.5.23;
e)
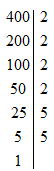
Vậy: 400=24.52400=24.52;
g) 1000000=26.561000000=26.56.
Vì 1000000=10.10.10.10.10.101000000=10.10.10.10.10.10
=2.5.2.5.2.5.2.5.2.5.2.5=2.5.2.5.2.5.2.5.2.5.2.5
Nên 1000000=2.5.2.5.2.5.2.5.2.5.2.5=26.561000000=2.5.2.5.2.5.2.5.2.5.2.5=26.56
Bài 127)
a)
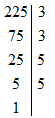
225=32.52225=32.52 chia hết cho 33 và 55;
b)

1800=23.32.521800=23.32.52 chia hết cho 2,3,52,3,5;
c)
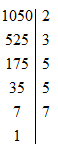
1050=2.3.52.71050=2.3.52.7 chia hết cho 2,3,5,72,3,5,7;
d)
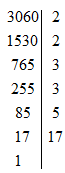
3060=22.32.5.173060=22.32.5.17 chia hết cho 2,3,5,172,3,5,17.
Bài 128)
44 là một ước của aa vì 44 là một ước của 2323;
8=238=23 là một ước của aa;
16=2416=24 không phải là ước của a;
1111 là một ước của aa;
2020 cũng là ước của aa vì 20=22.520=22.5 là ước của 23.5223.52.

cho tập hợp B={x,y,z}.Hỏi tập hợp B có bao nhiêu tập hợp con
bố mua cho em một quyển sổ tay dày 256 trang để tiện theo dõi em đánh số trang từ 1-256.Hỏi em phải viết bao nhiêu chữ số để đánh hết cuốn sổ tay
số nào là bội của 3 và là ước của 54
gọi A là tập hợp ước của 154.Hỏi A có số tập hợp con là

(149)@ ta có 60=2 mũ 2 nhân 3 nhân 5 280=2 mũ 3 nhân 5 nhân 7 BCNN (60,28 0)=2 mũ 3 nhân 3 nhân 5 nhân 7=840

ta có
12345678=1+2+3+4+5+6+7+8=36:hết cho 6(tổng 1 số chia hết 3 mà là số chẵn thì chia hết cho 6)
........
81234567: cho 6
=>biểu thức trên chia hết cho 6
Bạn j ơi, bạn hiểu sai ý mình rồi.
Ý mình là bạn phải tính biểu thức này cơ.
Chúc bạn may mắn lần sau.

Cách giải hệ phương trình bằng phương pháp đặt ẩn phụ
+ Bước 1: Đặt điều kiện để hệ phương trình có nghĩa
+ Bước 2: Đặt ẩn phụ thích hợp và đặt điều kiện cho ẩn phụ
+ Bước 3: Giải hệ theo các ẩn phụ đã đặt (sử dụng phương pháp thế hoặc phương pháp cộng đại số) sau đó kết hợp với điều kiện của ẩn phụ
+ Bước 4: Với mỗi giá trị ẩn phụ tìm được, tìm nghiệm tương ứng của hệ phương trình và kết hợp với điều kiện ban đầu
Đây bạn nhé!
A. Phương pháp giải
Bước 1: Đặt điều kiện của phương trình.
Bước 2: Đặt ẩn phụ, điều kiện của ẩn phụ. Đưa hệ ban đầu về hệ mới.
Bước 3: Giải hệ mới tìm ẩn phụ.
Bước 4: Thay giá trị vào ẩn phụ tìm x và y.
Bước 5: Kết luận.
⇒ Nếu hệ phương trình có biểu thức chứa căn hoặc phân thức chứa x và y thì phải có điều kiện xác định của hệ.
B. Ví dụ minh họa
Ví dụ : Giải hệ phương trình:
Hướng dẫn:

Bài 139.
a) Ta có 56 = 23 . 7; 140 = 22 . 5 . 7. Do đó ƯCLN(56,140) = 22 . 7 = 28;
b) Ta có 24 = 23 . 3; 84 = 22 . 3 . 7; 180 = 22 . 32 . 5.
Vậy ƯCLN(24,84,180) = 22 . 3 = 12.
c) Vì 180⋮60 nên ƯCLN(60,180) = 60;
d) ƯCLN(15,19) = 1.
Bài 140.
a) Vì 80⋮16 và 176⋮16 nên ƯCLN(16, 80, 176) = 16;
b) Ta có 18 = 2 . 32 ; 30 = 2 . 3 . 5; 77 = 7 . 11.
Do đó 18 , 30, 77 không có ước chung nào khác 1.
Vậy ƯCLN(18,30,77) = 1.