Định m để TXĐ của các hàm số sau là Ra| \(y=\dfrac{x+1}{x^2-m+6}\)b| \(y=\dfrac{2x+1...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TD

Truong Dung

11 tháng 7 2021

Định m để TXĐ của các hàm số sau là R

a| \(y=\dfrac{x+1}{x^2-m+6}\)

b| \(y=\dfrac{2x+1}{mx^2+4}\)

#Toán lớp 10

2

DH

Dưa Hấu

11 tháng 7 2021

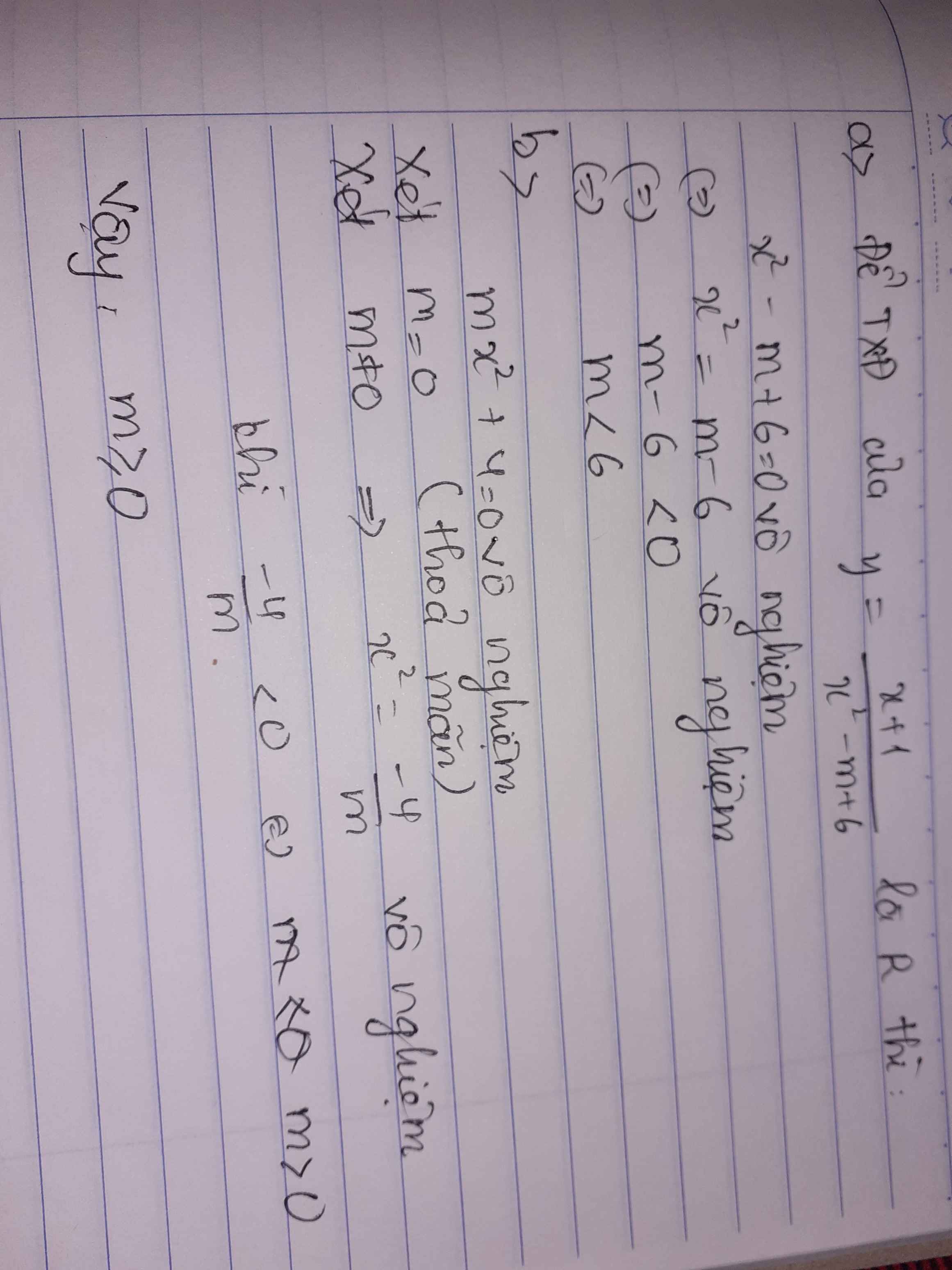
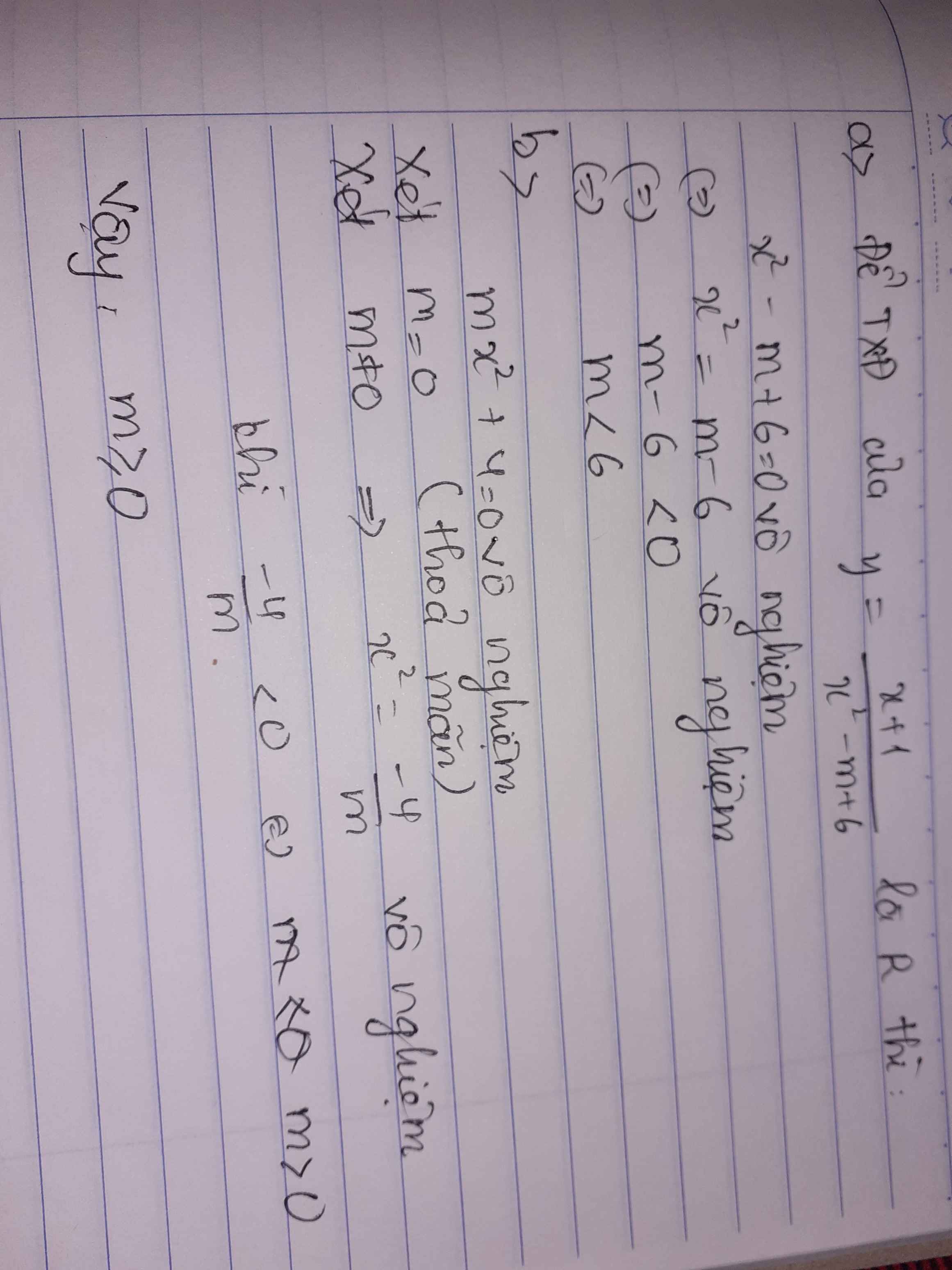
undefined

NL

Nguyễn Lê Phước Thịnh

11 tháng 7 2021

undefined

Các câu hỏi dưới đây có thể giống với câu hỏi trên

VT

Võ Thanh Nhung

6 tháng 12 2018

Tìm m để học sinh sau có TXĐ là P

a. y=\(\dfrac{1-x}{2x^2-x+m-2}\)

b. y=\(\dfrac{x-1}{x^2-4x-m+1}\)

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

30 tháng 11 2022

Sửa đề: TXĐ là R

a: Để hàm số sau có TXĐ là R thì 2x^2-x+m-2>0 với mọi x

=>\(\left\{{}\begin{matrix}\left(-1\right)^2-4\cdot2\left(m-2\right)< 0\\2>0\end{matrix}\right.\Leftrightarrow1-8m+16< 0\)

=>-8m+17<0

=>-8m<-17

=>m>17/8

b: Để hàm số có TXĐ là R thì x^2-4x-m+1>0 với mọi x

=>\(\left\{{}\begin{matrix}1>0\\\left(-4\right)^2-4\left(-m+1\right)< 0\end{matrix}\right.\Leftrightarrow16+4m-4< 0\)

=>4m+12<0

=>m<-3

CB

Cô bé Tinh Nghịch

14 tháng 7 2018

Tìm tham số m để hàm số

a, \(y=\dfrac{2x-1}{x^2-mx}\) xác định trên khoảng \(\left(0;2\right)\)

b, \(y=\sqrt{2x+m+1}+\dfrac{1}{x-m}\)xác định trên khoảng \(\left(1;+\infty\right)\)

#Toán lớp 10

0

BM

Bùi Minh

3 tháng 4 2020 - olm

cho hàm số y= \(\frac{2x-1}{\sqrt{mx^4+mx^3+\left(m+1\right)x^2+mx+1}}\).Hỏi có bn giá trị nguyên của m để hàm số xác định với mọi x thuộc R.

#Toán lớp 10

2

GR

ღ๖ۣۜCô ρɦươηɠ тự тɦưởηɠღ 《孤芳自赏...

3 tháng 4 2020

ĐKXĐ

\(mx^4+mx^3+\left(m+1\right)x^2+mx+1\)

\(=\left(mx^4+mx^3+mx^2+mx\right)+\left(x^2+1\right)\)

=\(mx\left(x^3+x^2+x+1\right)+\left(x^2+1\right)\)

\(=mx\left(x+1\right)\left(x^2+1\right)+\left(x^2+1\right)\)

\(=\left(x^2+1\right).\left[mx\left(x+1\right)+1\right]>0\left(\forall x\right)\)

\(=>mx^2+mx+1>0\left(\forall x\right)\)

\(=>PT\hept{\begin{cases}mx^2+mx+1=0\left(zô\right)nghiệm\forall x\\m>0\end{cases}}\)

\(\hept{\begin{cases}\Delta< 0\\m>0\end{cases}=>\hept{\begin{cases}m^2-4m< 0\\m>0\end{cases}=>\hept{\begin{cases}m\left(m-4\right)< 0\\m>0\end{cases}=>0< m< 4}}}\)

=> m có 3 giá trị là 1,2,3 nha

BM

Bùi Minh

5 tháng 4 2020

https://olm.vn/hoi-dap/detail/249896752542.html?pos=586036211459

giúp mk cả câu này

NN

Ngọc Nguyễn Ánh

25 tháng 7 2018

1. Timf a để hàm số y= \(\dfrac{2x+1}{x^2-6x+a-2}\) có tập xác định là R

2. Tìm m để hàm số y=\(\dfrac{2x}{x-m+1}\) xác định trên khoảng (0;2)

#Toán lớp 10

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 8 2022

Câu 1:

Để hàm số này có tập xác định là R thì \(x^2-6x+a-2>0\)

\(\text{Δ}=\left(-6\right)^2-4\left(a-2\right)=36-4a+8=44-4a\)

Để phương trình này luôn đúng với mọi x thì 44-4a<0

=>4a>44

=>a>11

DT

Đỗ Thị Kim Anh

22 tháng 12 2018

Bài 1 : Xác định :a, a và b để đồ thị hàm số y = ax +b đi qua điểm M(4; -3) và song song với đường thẳng d:\(y=-\dfrac{2}{3}x+1\) b, (P): \(y=ax^2+bx+c\) đi qua điểm A(1;1), B(-1;-3), O(0;0) Bài 2: xét sự biến thiên và vẽ đồ thị của hàm số sau : \(y=-x^2+2x+3\) Bài 3 : giải các phương trình sau : a,\(\dfrac{6x+3}{x+1}=\dfrac{2x+1}{x-1}\) b,...

#Toán lớp 10

3

DT

Đỗ Thị Kim Anh

22 tháng 12 2018

giúp mình với nha mọi người

TA

Trương Anh

28 tháng 12 2018

Bài 1 : Đồ thị đi qua điểm M(4;-3) \(\Rightarrow\) y=-3 x=4. Ta được:

\(-3=4a+b\)

Đồ thị song song với đường d \(\Rightarrow\) \(a=a'=-\dfrac{2}{3}\) Ta được:

\(-3=4.-\dfrac{2}{3}+b\) \(\Rightarrow\) \(b=-\dfrac{1}{3}\)

Vậy: \(a=-\dfrac{2}{3};b=-\dfrac{1}{3}\)

b) (P) đi qua 3 điểm A B O, thay tất cả vào (P), ta được hpt:

\(\hept{\begin{cases}a+b+c=1\\a-b-c=-3\\0+0+1=0\end{cases}\Leftrightarrow\hept{\begin{cases}a=-1\\b=2\\c=0\end{cases}}}\)

Bài 2 : Mình ko biết vẽ trên này, bạn theo hướng dẫn rồi tự làm nhé

Đồ thị có \(a< 0\) \(\Rightarrow\) Hàm số nghịch biến trên R

\(\Rightarrow\) Đồ thị có đỉnh \(I\left(1;4\right)\)

Chọn các điểm:

x 1 3 -1 2 -2

y 4 0 0 3 -5

H

Hiếu

8 tháng 5 2019

1,Tìm m để x2 - mx + m + 3 ≥ 0 có tập nghiệm là R A. (-6;2) B.(-∞;6) ∪ (2;+∞) C. [-6;2] D. (-∞;-6] ∪ [2;+∞) 2, Tìm m để mx2 - 4(m+1)x + m - 5 > 0 vô nghiệm A. m ∈ (-1;\(\dfrac{-1}{3}\) ) B. m ∈ [-1;\(\dfrac{-1}{3}\)] C. m ∈ (-∞;0) D. m ∈ (-∞;-1] ∪ [\(\dfrac{-1}{3}\);+∞) 3, Tìm m để -2x2 + 2(m-2)x + m - 2 = 0 có hai nghiệm phân biệt A. m ∈ (0;\(\dfrac{1}{2}\)) B. m ∈ (-∞;0) ∪...

#Toán lớp 10

1

NV

Nguyễn Việt Lâm

Giáo viên

9 tháng 5 2019

Câu 1:

\(\Delta=m^2-4\left(m+3\right)\le0\)

\(\Leftrightarrow m^2-4m-12\le0\Rightarrow-2\le m\le6\)

Câu 2:

Để BPT đã cho vô nghiệm tương đương \(mx^2-4\left(m+1\right)x+m-5\le0\) đúng với mọi x

\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\\Delta'=4\left(m+1\right)^2-m\left(m-5\right)\le0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m< 0\\3m^2+13m+4\le0\end{matrix}\right.\) \(\Leftrightarrow-4\le m\le-\frac{1}{3}\)

Tất cả các đáp án đều sai

Câu 3:

Để pt có 2 nghiệm pb

\(\Leftrightarrow\Delta'=\left(m-2\right)^2+2\left(m-2\right)>0\)

\(\Leftrightarrow m^2-2m>0\Leftrightarrow\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\)

Tiếp tục tất cả các đáp án đều sai, đề bài gì kì vậy ta

M

masterpro

25 tháng 8 2021 - olm

Cho hàm số y=\(\sqrt{x^4-x^2+1+mx\sqrt{2x^4+2}}.\) . Tìm tất cả các giá trị của tham số m để hàm số có tập xác định là tập số thực R. GIẢI GIÚP MÌNH VỚI!!

#Toán lớp 10

0

Y

YếnChiPu

30 tháng 4 2018

1, c/m vs x\(\ne\dfrac{k\pi}{2},k\in Z\)

\(\dfrac{1+\sin^4x-\cos^4x}{1-\sin^6x-\cos^6x}=\dfrac{2}{3cos^2x}\)

2, TÌM tất cả các gt của tham số ,để h/s sau có tập xđ D=R

y=\(\sqrt{mx^2-2\left(m+1\right)x+4}\\ \)

#Toán lớp 10

1

CC

Chí Cường

28 tháng 8 2018

\(\dfrac{1+sin^4x-cos^4x}{1-sin^6x-cos^6x}=\dfrac{1+sin^2x-cos^2x}{1-\left(sin^4x+cos^4x-sin^2xcos^2x\right)}=\dfrac{1+sin^2x-\left(1-sin^2x\right)}{1-\left(1-3sin^2xcos^2x\right)}=\dfrac{2sin^2x}{3sin^2xcos^2x}=\dfrac{2}{3cos^2x}\)

PC

Pun Cự Giải

6 tháng 10 2018

Tìm TXĐ của các hàm số

a) \(y=\sqrt{x-1}+\dfrac{1}{x+3}\)

b) \(y=\sqrt{\left|2x-1\right|}\)

c) y= \(\sqrt{2x-3}+\dfrac{1}{3-x}\)

#Toán lớp 10

2

ND

Nguyen Duy Lap

18 tháng 10 2018

a) D= (1; +oo)
b) D= R
c)D = (3/2; +oo) / {3}

NL

Nguyễn Lê Phước Thịnh

8 tháng 10 2022

a: ĐKXĐ: x-1>=0 và x+3<>0

=>x>=1 và x<>-3

=>D=[1;+\(\infty\))

b: TXĐ: D=R

c: ĐKXĐ: 2x-3>=0 và 3-x<>0

=>x>=3/2 và x<>3