Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐKXĐ : \(\hept{\begin{cases}2x+1\ne0\\3+x\ne0\end{cases}}\Leftrightarrow\hept{\begin{cases}x\ne-\frac{1}{2}\\x\ne-3\end{cases}}\)

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo để được hỗ trợ tốt hơn. Viết ntn nhìn rất khó đọc
1: =>x-3+3x-9-2(3-x)=60
=>4x-12-6+2x=60
=>6x-18=60
=>6x=78
=>x=13
2: ĐKXĐ: x<>-1; x<>3

a) ĐKXĐ: : x ≠ 1 và x ≠ -1.
b) Quy đồng và khử mẫu ta được PT: x(x + 1) = (x – 1)(x +4)
⇔ x2 +x = x2 +4x– x -4
⇔ x – 4x +x = -4 -2x = -4 x = 2(thỏa mãn ĐKXĐ)
Vậy PT có tập nghiệm S = {2}

+ Pt thứ nhất :
Ta có mẫu thức chung là : \(2\left(x-3\right)\left(x+1\right)\)
\(\Rightarrow\left[{}\begin{matrix}x\ne2\\x-3\ne0\\x+1\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne3\\x\ne-1\end{matrix}\right.\)
Vậy \(ĐKXĐ\) là :\(x\ne2;3;-1\)
+ Pt thứ hai :
Ta có mẫu thức chung là : \(\left(x-2\right)\left(x+3\right)\)
\(\Rightarrow\left[{}\begin{matrix}x-2\ne0\\x+3\ne0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)
Vậy \(DKXD:\) \(\) \(x\ne2;-3\)

Ta thấy x + 2 ≠ 0 khi x ≠ - 2 và x - 2 ≠ 0 khi x ≠ 2.
Do đó ĐKXĐ của phương trình (x - 1)/(x + 2) + 1 = 1/(x - 2) là x ≠ ± 2.

1B
2D
3A
4A
5B
6:
a: \(A=\dfrac{14+2}{3}=\dfrac{16}{3}\)
b: P=A*B
\(=\dfrac{x+2}{3}\cdot\dfrac{2x^2+6x-2x^2-3x-9}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x+2}{3}\cdot\dfrac{3x-9}{\left(x-3\right)\left(x+3\right)}=\dfrac{x+2}{x+3}\)
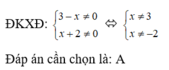
ĐKXĐ: 3 - x ≠ 0 ⇔ x ≠ 3