Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=2021\cdot2\cdot\left(1+\dfrac{1}{2}:\dfrac{3}{2}-\dfrac{4}{3}\right)=4042\cdot\left(1+\dfrac{1}{3}-\dfrac{4}{3}\right)=0\)

\(\dfrac{2021}{2022}\) x \(\dfrac{2022020222022}{202320232023}\) x \(\dfrac{20212021}{20232023}\)
= \(\dfrac{2021}{2022}\) x \(\dfrac{2022}{2023}\) x \(\dfrac{2021}{2023}\)
= \(\dfrac{2021\times2021}{2023\times2023}\)
= \(\dfrac{4084441}{4092529}\)

Nhỏ hơn
Ta có 2020/2021 <1
2021/2022 <1
2022/2023 <1
2023/2024 <1
Suy ra A=(2021/2021+2021/2022 +2022/2023 +2023/2024) < (1+1+1+1)= 4
Vậy A <4
Chúc bạn học tốt
\(\dfrac{2020}{2021}< 1\)
\(\dfrac{2021}{2022}< 1\)
\(\dfrac{2021}{2022}< 1\)
\(\dfrac{2023}{2024}< 1\)
Do đó: A<4

\(2022\times2005-2000\times2022+15\times2022-20\times2021\)
\(=2022\times\left(2005-2000+15\right)-20\times2021\)
\(=2022\times20-20\times2021\)
\(=20\times\left(2022-2021\right)\)
\(=20\times1\)
\(=20\)
a, 2022 \(\times\) 2005 - 2000 \(\times\) 2022 + 15 \(\times\) 2022 - 20 \(\times\) 2021
= (2022 \(\times\) 2005 - 2000 \(\times\) 2022 + 15 \(\times\) 2022 )- 20 \(\times\) 2021
= 2022 \(\times\) (2005 - 2000 + 15) - 20 \(\times\) 2021
= 2022 \(\times\) (5 +15) - 20 \(\times\) 2021
= 2022 \(\times\) 20 - 20 \(\times\) 2021
= 20 \(\times\) (2022 - 2021)
= 20 \(\times\) 1
= 20

Không cần tính, ta thấy : 2022/2021 > 2021/2022
Vậy : 2022/2021*2023 > 2021/2022*2022

Ta có:
\(A=\frac{2021^{2021}+1}{2021^{2022}+1}\Leftrightarrow10A=\frac{2021^{2022}+10}{2021^{2022}+1}=1+\frac{9}{2021^{2022}+1}\)
\(B=\frac{2021^{2022}-1}{2021^{2023}-1}\Leftrightarrow10B=\frac{2021^{2023}-10}{2021^{2023}-1}=1-\frac{9}{2021^{2023}-1}\)
Hay ta đang so sánh: \(\frac{9}{2021^{2022}};\frac{9}{2021^{2023}}\)
Mà \(\frac{9}{2021^{2022}}>\frac{9}{2021^{2023}}\)nên \(\frac{2021^{2021}+1}{2021^{2022}+1}>\frac{2021^{2022}-1}{2021^{2023}-1}\)hay\(A>B\)
Vậy \(A>B\)


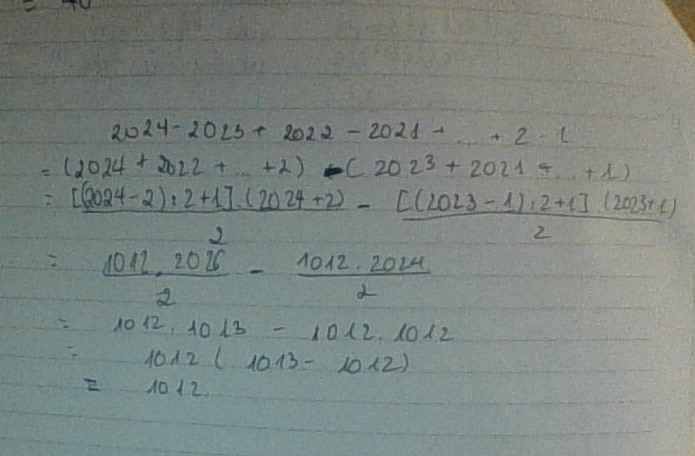
504
Chỉ cho tớ cách làm đc ko? Tại nay gặp bài này rối quá.