Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AD = AE nên A nằm trên tia phân giác của góc xOy
BM = BN nên B nằm trên tia phân giác của góc xOy
Mà A ≠ B nên đường thẳng AB là đường phân giác của góc xOy.

moy cau nay de nhung minh khong biet ve hinh tren may tinh
Vẽ hình này khó lắm nhưng nếu bạn suy nghĩ thêm 1 xíu là ra ngay thui , cố lên ^^

a ) Ta có : \(\widehat{xOy}+\widehat{x'Oy}=180^0\)
\(\Rightarrow\widehat{x'Oy}=180-60=120^0\)
Ta có :
\(\widehat{x'Oy}+\widehat{x'Oy'}=180\)
\(\Rightarrow\widehat{x'Oy'}=180-120=60^0\)
Ta lại có :
\(\widehat{x'Oy'}+\widehat{xOy'}=180^0\)
\(\Rightarrow\widehat{xOy'}=180-60=120^0\)
b ) Ta có : \(\widehat{xOy}=\widehat{x'Oy'}=60^0\)
\(\Rightarrow\) Tia phân giác của \(\widehat{xOy}=\widehat{x'Oy'}\)\(\Rightarrow Om\) và \(On\) là hai tia đối nhau .
Bạn tự vẽ hình nha ==''
a.
xOy = x'Oy' (2 góc đối đỉnh)
mà xOy = 600
=> x'Oy' = 600
xOy + yOx' = 1800 (2 góc kề bù)
600 + yOx' = 1800
yOx' = 1800 - 600
yOx' = 1200
mà yOx' = y'Ox (2 góc đối đỉnh)
=> y'Ox = 1200
b.
Om là tia phân giác của xOy
=> xOm = mOy = xOy/2
On là tia phân giác của x'Oy'
=> x'On = nOy' = x'Oy'/2
mà xOy = x'Oy' (2 góc đối đỉnh)
=> xOm = x'On
mà xOn + nOx' = 1800 (2 góc kề bù)
=> xOn + xOm = 1800
=> xOn và xOm kề bù
=> On và Om là 2 tia đối
Chúc bạn học tốt ^^

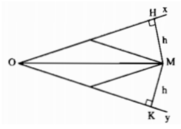
Kẻ MH ⊥ Ox, MK ⊥ Oy.
Khi đó:
MH là chiều rộng của thước hai lề
MK là chiều rộng của thước hai lề
Mà chiều rộng của thước đó bằng nhau và bằng h nên ta có:
MH = MK = h
Điểm M nằm trong góc xOy và cách đều hai cạnh của góc nên M thuộc tia phân giác của góc xOy.

Bài 1
a
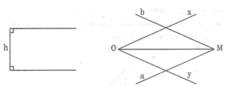
Ta có:
\(\widehat{O_1}=\widehat{O_2}=60^0\left(đ.đ\right)\)
\(\widehat{O_1}+\widehat{O_2}=180^0\Rightarrow\widehat{0_2}=180^0-\widehat{O_1}=180-60^0=120^0\)
\(\widehat{O_2}=\widehat{O_4}=120^0\left(đ.đ\right)\)
b
Ta có:
\(\widehat{x'Oy}=\widehat{y'Ox}\Rightarrow\frac{1}{2}\widehat{x'Oy}=\frac{1}{2}\widehat{y'Ox}\Rightarrow\widehat{yOn}=\widehat{xOm}\)
\(\widehat{x'Oy}+\widehat{yOx}=180^0\)
\(\Rightarrow2\cdot\widehat{yOn}+\widehat{yOx}=180^0\)
\(\Rightarrow\widehat{yOn}+\widehat{yOx}+\widehat{xOm}=180^0\)
\(\Rightarrowđpcm\)
Bài 2
a
Ta có:
\(\widehat{BOD}=\widehat{AOC}=90^0\Rightarrow\widehat{BOC}+\widehat{COD}=\widehat{AOD}+\widehat{COD}\Rightarrow\widehat{BOC}=\widehat{AOD}\)
b
Ta có:
\(\widehat{BOM}=\widehat{BOC}+\widehat{COM}=\widehat{AOD}+\widehat{MOD}=\widehat{MOA}\)
Hiển nhiên OM nằm giữa \(\widehat{AOB}\) nên suy ra đpcm

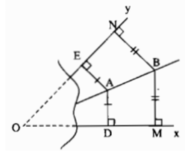
Vì AD=AE
nên A nằm trên đường phân giác của góc xOy
Vì BM=BN
nên B nằm trên đường phân giác của góc xOy
=>AB là phân giác của góc xOy