Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

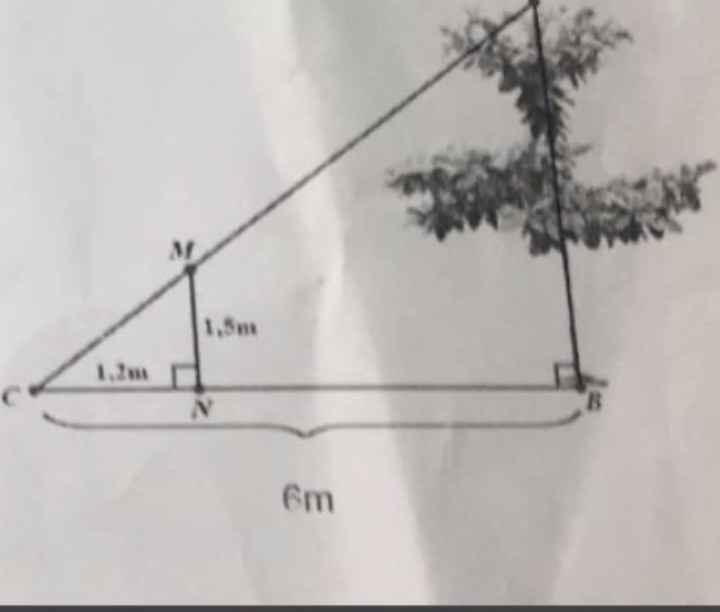
Ta có:MN\(\perp\)CB
AB\(\perp\)CB
Do đó: MN//AB
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CN}{CB}\)
=>\(\dfrac{1.5}{AB}=\dfrac{1.2}{6}=\dfrac{1}{5}\)
=>AB=1,5*5=7,5(m)

Cậu tham khảo đường link này là ra, dạng tương tự
https://h.vn/hoi-dap/tim-kiem?q=B%C3%A0i+53+(Sgk+t%E1%BA%ADp+2+-+trang+87)M%E1%BB%99t+ng%C6%B0%E1%BB%9Di+%C4%91o+chi%E1%BB%81u+cao+c%E1%BB%A7a+m%E1%BB%99t+c%C3%A2y+nh%E1%BB%9D+m%E1%BB%99t+c%E1%BB%8Dc+ch%C3%B4n+xu%E1%BB%91ng+%C4%91%E1%BA%A5t,+c%E1%BB%8Dc+cao+2m+v%C3%A0+%C4%91%E1%BA%B7t+xa+c%C3%A2y+15m.+Sau+khi+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+l%C3%B9i+ra+xa+c%C3%A1ch+c%E1%BB%8Dc+0,8m+th%C3%AC+nh%C3%ACn+th%E1%BA%A5y+%C4%91%E1%BA%A7u+c%E1%BB%8Dc+v%C3%A0+%C4%91%E1%BB%89nh+c%C3%A2y+c%C3%B9ng+n%E1%BA%B1m+tr%C3%AAn+m%E1%BB%99t+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng.+H%E1%BB%8Fi+c%C3%A2y+cao+bao+nhi%C3%AAu,+bi%E1%BA%BFt+r%E1%BA%B1ng+kho%E1%BA%A3ng+c%C3%A1ch+t%E1%BB%AB+ch%C3%A2n+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+%C4%91%E1%BA%BFn+m%E1%BA%AFt+ng%C6%B0%E1%BB%9Di+%E1%BA%A5y+l%C3%A0+1,6m+?&id=247547

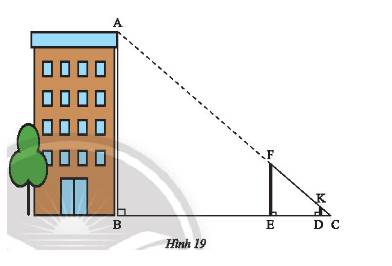
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.

a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
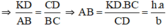
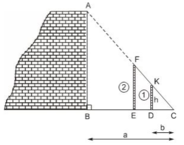
Vậy chiều cao bức tường là 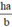

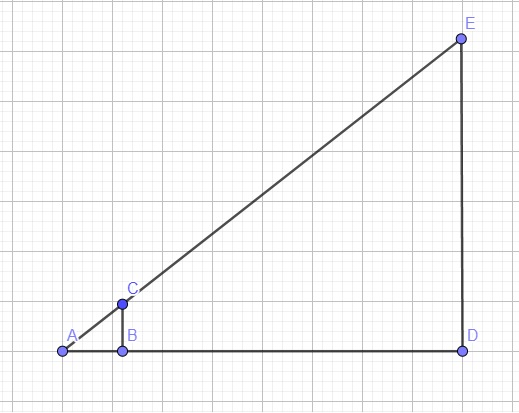
Đặt tên các điểm như hình vẽ.
Ta có \(AB=0,8\left(m\right)\), \(BD=15\left(m\right)\), \(BC=2\left(m\right)\)
Do \(BC||DE\) (cùng vuông góc mặt đất AD)
Áp dụng định lý Thales:
\(\dfrac{AB}{AD}=\dfrac{BC}{DE}\Rightarrow\dfrac{0,8}{0,8+15}=\dfrac{2}{DE}\)
\(\Rightarrow DE=\dfrac{2.15,8}{0.8}=39,5\left(m\right)\)

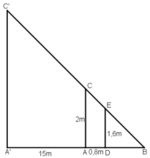
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB  ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB  ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
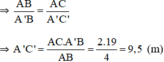
Vậy cây cao 9,5m.

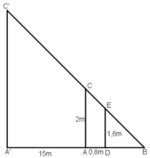
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB  ΔACB (vì DE // AC)
ΔACB (vì DE // AC)

Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB  ΔA’C’B (vì AC // A’C’)
ΔA’C’B (vì AC // A’C’)
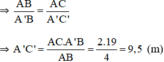
Vậy cây cao 9,5m.
có pk kiến thức lớp 8 k.o v
chứ lớp mấy:3