Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn B.
Vì trong môi trường trong suốt và đồng tính ánh sáng truyền theo đường thẳng. Do vậy ánh sáng từ bóng đèn pin truyền qua lỗ thủng nhỏ O sau đó là truyền thẳng tới H. Vì vậy đặt mắt ở vị trí H bên kia tấm bìa có thể nhìn thấy dây tóc bóng đèn.

Đặt mắt sau 3 tấm bìa có đục lỗ để nhìn ánh sáng từ ngọn đèn. Nếu ba lỗ không thẳng hàng, mắt không nhìn thấy ánh sáng từ ngọn đèn truyền tới.
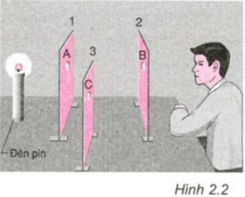
Ta luồn một sợi dây (hay một cây thước thẳng) qua 3 lỗ A B C
+ Nếu 3 lỗ A, B, C và bóng đèn cùng nằm trên đường thẳng chứa sợi dây đó thì chúng thẳng hàng
+ Nếu 3 lỗ A, B, C và bóng đèn không cùng nằm trên đường thẳng chứa sợi dây đó thì chúng không thẳng hàng
Kết luận: Đường truyền của ánh sáng trong không khí là đường thẳng.

C1: Dùng một dây chỉ luồn qua ba lỗ A, B, C rồi căng thẳng dây.
C2: Luồn một que nhỏ thẳng qua ba lỗ để xác nhận ba lỗ thẳng hàng.
Vậy đường truyền của ánh sáng trong không khí là đường thẳng.
C1: Dùng một dây chỉ luồn qua ba lỗ A, B, C rồi căng thẳng dây.
C2: Luồn một que nhỏ thẳng qua ba lỗ để xác nhận ba lỗ thẳng hàng.
Vậy đường truyền của ánh sáng trong không khí là đường thẳng.

Tóm tắt:
ST = d; SM = 1/4d; Bìa có bán kính R
a) Tìm R’
b) MM1 = ? để R’’ = ½ R’. Tìm v’ của bóng đen nếu đèn có vận tốc v
c) thay S bằng nguồn sáng có bán kính r. Tìm Sđen và Snửa tối.
Bài giải
Ta có hình vẽ
a) Bán kính vùng tối trên tường là PT
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên 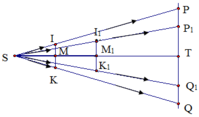
a) Bán kính vùng tối trên tường là PT
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên
⇒ I M P T = S M S T ⇔ P T = S T S M . I M = d 1 / 4 d . R = 4 R
b) Từ hình vẽ ta thấy để bán kính vùng tối giảm xuống ta phải di chuyển tấm bìa về phía tường.
Gọi P1T là bán kính bóng đen lúc này P1T = 1/2PT = 2R
∆SIM và ∆SPT là 2 tam giác vuông đồng dạng nên
![]()
Vậy cần di chuyển tấm bìa về phía tường một đoạn
M1M = SM1 - SM= 1 2 d - 1 4 d = 1 4 d
Khi tấm bìa di chuyển đều với vận tốc v và đi được quãng đường M1M = 1/4d thì mất thời gian t = M 1 M v = d 4 v
Cũng trong khoảng thời gian đó bán kính của vùng tối thay đổi một đoạn là
PP1 = PT – P1T = 4R – 2R = 2R
Vậy tốc độ thay đổi của bán kính vùng tối là P 1 P t = 2 R d 4 v = 8 R v d
c) Thay điểm sáng S bằng nguồn sáng hình cầu. Ta có hình vẽ
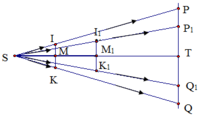
Gọi AB là đường kính nguồn sáng, O là tâm nguồn sáng. Theo kết quả câu b) M là trung điểm của ST.
Bán kính vùng tối là PT, ta có ∆BIC = ∆ PID (g.c.g) => PD = BC.
Mà ta lại có BC = OC – OB = MI – OB = R-r.
PT = PD + DT = BC + IM = (R-r) + R = 2R – r
Vậy diện tích vùng tối trên tường là: STối = π.(2R – r)2
Vùng nửa tối là diện tích hình vành khăn có bán kính lớn là P’T, bán kính nhỏ là PT
Ta có: ∆ AIC = ∆P’ID (g.c.g) ⇒ P’D = AC = R+r
Mà: P’T = P’D + IM = AC + IM = R+r + R = 2R+r
Từ đó ta có: Diện tích vùng nửa tối là:
SNửa tối = π.(2R + r)2 - π.(2R - r)2 = 8πRr

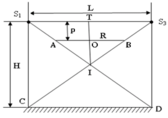
Để khi quạt quay, không một điểm nào trên sàn bị sáng loang loáng thì bóng của đầu mút quạt chỉ in trên tường và tối đa là đến chân tường C và D.
Vì nhà hình hộp vuông, ta chỉ xét trường hơph cho một bóng, các bóng còn lại là tương tự (Xem hình vẽ bên)
Gọi L là đường chéo của trần nhà :
L = 4 2 » 5,7m
Khoảng cách từ bóng đèn đến chân tường đối diện là :
S1D = H 2 + L 2 = ( 3 , 2 ) 2 + ( 4 2 ) 2 = 6 , 5 m
T là điểm treo quạt, O là tân quay của cánh quạt. A, B là các đầu mút khi cánh quạt quay. Xét DS1IS3 ta có :
A B S 1 S 2 = O I I T ⇒ O I = A B S 1 S 2 . I T = 2 R . H 2 L = 2.0 , 8. 3 , 2 2 5 , 7 = 0 , 45 m
Khoảng cách từ quạt đến điểm treo là : OT = IT – OI = 1,6 – 0,45 = 1,15 m.
Vậy quạt phải treo cách trần nhà tối đa là 1,15 m.

Tóm tắt:
SI = 2m = 200 cm
R = 0,5m = 50 cm
Rtối = 60 cm
Tìm SM
Bài làm:
Ta có hình vẽ:
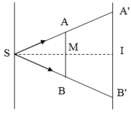
Bán kính vùng tối là A’I, bán kính vật chắn là AM.
Ta có tam giác ∆ SAM ~ ∆ SA’I nên ta có:
S M S I = A M A ' I ⇒ S M = S I . A M A ' I = 200. 50 60 = 166 , 67 c m
Vậy phải đặt vật chắn sáng cách đèn là 166,67 cm.